题目内容
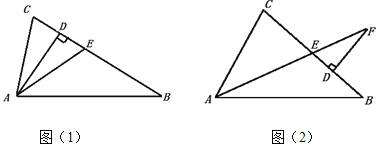
【题目】(1)如图(1),在△ABC中,AD、AE分别是△ABC的高和角平分线,已知:∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),∠BAC的角平分线AF交BC于点E,过点F作FD⊥BC于点D,若∠B = x°,∠C =(x+30)° .
①∠CAE = (含x的代数式表示)②求∠F的度数.
【答案】(1)∠DAE = 10° ;(2) ①∠CAE = (75-x) °,② ∠F =15°
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
(2)根据题意可知∠B=x°,∠C=(x+30)°,根据三角形的内角和定理可知∠ADC+∠DAC+∠C=180°,∠ADC=∠B+∠BAF,根据角平分线的性质,可知∠EAC=∠BAF,可得出∠ADC的度数,再根据FD⊥BC,可得出∠F的度数.
试题解析:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°-∠B-∠C=100°,
∵AD是△ABC角平分线,
∴∠CAE=![]() ∠CAB=50°,
∠CAB=50°,
∵AE是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°;
(2)①∵∠B=x°,∠C=(x+30)°,AF平分∠BAC,
∴∠EAC=∠BAF,
∴∠CAE=![]() ×[180°-x°-(x+30)°]=75°-x°,
×[180°-x°-(x+30)°]=75°-x°,
②∠AEC=∠BAE+∠B=75°,
∵FD⊥BC,
∴∠F=15°.

练习册系列答案
相关题目