题目内容
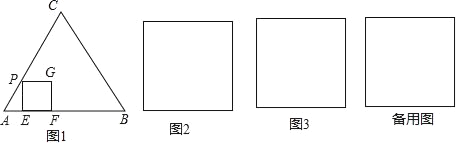
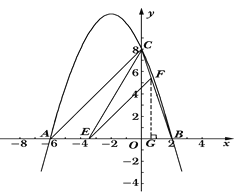
【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
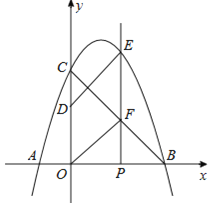
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
【答案】解:(1)∵点A(﹣1,0)、B(3,0)在抛物线y=ax2+bx+3上,
∴![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为:y=﹣x2+2x+3。
(2)在抛物线解析式y=﹣x2+2x+3中,令x=0,得y=3,∴C(0,3)。
设直线BC的解析式为y=kx+b,
将B(3,0),C(0,3)坐标代入得:![]() ,解得
,解得![]() 。
。
∴直线BC的解析式为y=﹣x+3。
设E点坐标为(x,﹣x2+2x+3),则P(x,0),F(x,﹣x+3)。
∴EF=yE﹣yF=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x。
∵四边形ODEF是平行四边形,∴EF=OD=2。
∴﹣x2+3x=2,即x2﹣3x+2=0,解得x=1或x=2。
∴P点坐标为(1,0)或(2,0)。
(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点A与![]() ODEF对称中心的直线平分
ODEF对称中心的直线平分![]() ODEF的面积。
ODEF的面积。
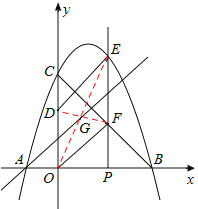
①当P(1,0)时,点F坐标为(1,2),
又D(0,2),
设对角线DF的中点为G,则G(![]() ,2)。
,2)。
设直线AG的解析式为y=k1x+b1,
将A(﹣1,0),G(![]() ,2)坐标代入得:
,2)坐标代入得: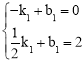 ,解得
,解得![]() 。
。
∴所求直线的解析式为:![]() 。
。
②当P(2,0)时,点F坐标为(2,1),又D(0,2)。
设对角线DF的中点为G,则G(1,![]() )。
)。
设直线AG的解析式为y=k2x+b2,
将A(﹣1,0),G(1,![]() )坐标代入得:
)坐标代入得: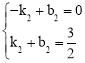 ,解得
,解得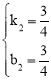 。
。
∴所求直线的解析式为![]() 。
。
综上所述,所求直线的解析式为![]() 或
或![]() 。
。
【解析】
试题(1)利用待定系数法求出抛物线的解析式。
(2)平行四边形的对边相等,因此EF=OD=2,据此列方程求出点P的坐标。
(3)利用中心对称的性质求解:平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点A与![]() ODEF对称中心的直线平分
ODEF对称中心的直线平分![]() ODEF的面积。
ODEF的面积。