题目内容
【题目】如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE;(填空)
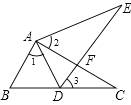
证明:∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2=∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
【答案】见解析.
【解析】
求出∠E=∠C,∠BAC=∠DAE,然后利用“角边角”证明△ABC和△ADE全等即可.
证明:∵∠2+∠E+∠AFE=180°(三角形的内角和等于180°)
∠3+∠C+∠CFD=180°(理由同上)
又∵∠2=∠3(已知)
∠AFE=∠CFD(对顶角相等)
∴∠E=∠C
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠__CAD _.
即∠BAC=∠DAE
在△ABC和△ADE中

∴△ABC≌△ADE(ASA)

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
【题目】某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏:如图所示,将一个正方形均分成9等份,数字的背面写有祝福语或奖金数.游戏规则是:每次翻动正面一个数字,看看反面对应的内容,就可知是得奖还是得到温馨祝福.
正面:
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
反面:
祝你开心 | 万事如意 | 奖金1 000元 |
身体健康 | 心想事成 | 奖金500元 |
奖金100元 | 生活愉快 | 谢谢参与 |
请你完成下列问题:
(1)翻到奖金1 000元的概率是多少?
(2)翻不到奖金的概率是多少?
(3)一选手准备在奇数中选择一个数字,他获得奖金的概率是多少?










