题目内容
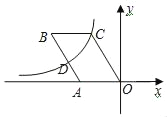
【题目】如图（1）是某公园里的一种健身器材，其侧面示意图如图（2）所示，其中AB=AC=120cm，BC=80cm，AD=30cm，∠DAC=90°．求点D到地面的高度是多少？
【答案】D到地面的高度为（10+
）cm
【解析】
过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．先得出AF的长，再利用相似三角形的判定与性质得出AH的长即可得出答案．
解：过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．
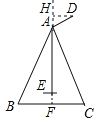
∵AF⊥BC
∴BF=FC=
BC=40cm．
根据勾股定理，得AF=
（cm），
∵∠DHA=∠DAC=∠AFC=90°，
∴∠DAH+∠FAC=90°，∠C+∠FAC=90°，
∴∠DAH=∠C，
∴△DAH∽△ACF，
∴
∴
，
∴AH=10cm.
∴HF=（10+）cm ,
答：D到地面的高度为（10+）cm．
故答案为：D到地面的高度为（10+）cm.
练习册系列答案
相关题目
