题目内容
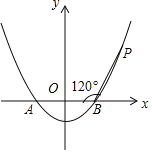
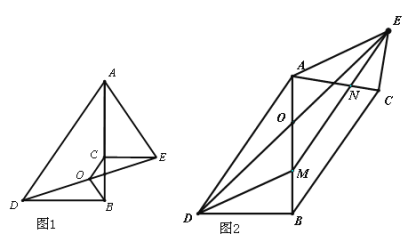
【题目】如图1,已知:△ABD∽△ACE,∠ABD=∠ACE=90°,连接DE,O是DE的中点。
(1)连接OC,OB 求证:OB=OC;
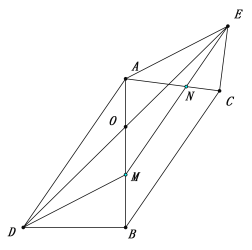
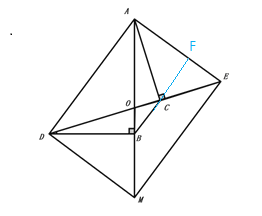
(2)将△ACE绕顶点A逆时针旋转到图2的位置,过点E作EM∥AD交射线AB于点M,交射线AC于点N,连接DM,BC. 若DE的中点O恰好在AB上。
①求证:△ADM∽△AEN
②求证:BC∥AD
③若AC=BD=3,AB=4,△ACE绕顶点A旋转的过程中,是否存在四边形ADME矩形的情况?如果存在,直接写出此时BC的值,若不存在说明理由。
【答案】(1)详见解析;(2)①详见解析;②详见解析;③存在四边形ADME为矩形,此时BC=![]()
【解析】
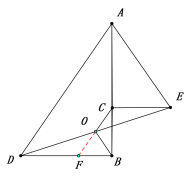
(1)延长CO交BD于点F,可证△CEO≌△FDO,则OC=OF,再根据直角三角形斜边上的中线等于斜边的一半即可求解;
(2)①根据平行的性质得∠DAM=∠EMA,可证△AOD≌△MOE,则AD=EM,根据平行四边形的判定定理可判断ADME是平行四边形,由平行四边形的性质可得∠ADM=∠AEN,由△ABD∽△ACE可得∠BAD=∠CAE,即可证△ADM∽△AEN;
②根据相似三角形对应边成比例可得![]() ,由比例的性质得
,由比例的性质得![]() ,因为∠MAN=∠BAC,根据相似三角形的判定定理可证出△AMN∽△ABC,则∠AMN=∠ABC,根据同位角相等,两直线平行可得MN∥BC,根据平行于同一条直线的两直线平行可得BC∥AD;
,因为∠MAN=∠BAC,根据相似三角形的判定定理可证出△AMN∽△ABC,则∠AMN=∠ABC,根据同位角相等,两直线平行可得MN∥BC,根据平行于同一条直线的两直线平行可得BC∥AD;
③存在四边形ADME为矩形,此时BC=![]() ,如图,延长BC交AE于F,求出BF=
,如图,延长BC交AE于F,求出BF=![]() ,CF=
,CF=![]() ,即可求得BC的值.
,即可求得BC的值.
解:(1)延长CO交BD于点F
∵∠ABD=∠ACE=90°
∴CE∥BD
∴∠CEO=∠FDO
∵O是DE的中点
∴OE=OD
∵∠COE=∠DOF
∴△CEO≌△FDO
∴OC=OF
∵∠CBF=90°
∴BO=![]() CF=OC ;
CF=OC ;
(2)①∵O是DE的中点
∴OE=OD
∵EM∥AD
∴∠DAM=∠EMA
∵∠AOD=∠MOE
∴△AOD≌△MOE
∴AD=EM
∵EM∥AD
∴四边形ADME是平行四边形
∴∠ADM=∠AEN
∵△ABD∽△ACE
∴∠BAD=∠CAE
∴△ADM∽△AEN ;
②∵△ADM∽△AEN
∴![]()
∵△ABD∽△ACE
∴![]()
∴![]()
∴![]()
∵∠MAN=∠BAC
∴△AMN∽△ABC
∴∠AMN=∠ABC
∴MN∥BC
∵MN∥AD
∴BC∥AD ;
③ 如图,存在四边形ADME为矩形,此时BC=![]() .
.
故答案为:(1)详见解析;(2)①详见解析;②详见解析;③存在四边形ADME为矩形,此时BC=![]() .
.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?