题目内容
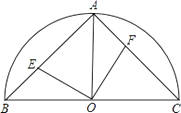
【题目】如图![]() ,已知
,已知![]() ,点
,点![]() ,
, ![]() 分别是射线
分别是射线![]() ,
, ![]() 上两定点,且
上两定点,且![]() ,
, ![]() ;动点
;动点![]() 从点
从点![]() 向点
向点![]() 运动,以
运动,以![]() 为斜边向右侧作等腰直角
为斜边向右侧作等腰直角![]() .设线段
.设线段![]() 的长
的长![]() ,点
,点![]() 到射线
到射线![]() 的距离为
的距离为![]() .
.
(1)若![]() ,直接写出点
,直接写出点![]() 到射线
到射线![]() 的距离;
的距离;
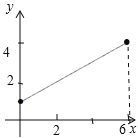
(2)求![]() 关于
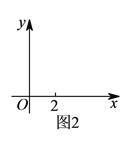
关于![]() 的函数表达式,并在图
的函数表达式,并在图![]() 中画出函数图象;
中画出函数图象;
(3)当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,求点
,求点![]() 运动经过的路径长.
运动经过的路径长.

【答案】(1)2;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)OB=2时,四边形OACB是正方形,由此即可解决问题.
(2)如图,作CE⊥OA于E,CF⊥ON于F.由△CEA≌△CFB,推出AE=CF,CE=CF,由∠CEO=∠CFO=∠EOF=90°,推出四边形OECF是矩形,由CE=CF,推出四边形OECF是正方形,根据AE=y-2,FB=x-y,可得y-2=x-y,即y=![]() x+1(0≤x≤6),画出图象即可.
x+1(0≤x≤6),画出图象即可.
(3)如图,由CE=CF,推出OC平分∠MON,推出点C的运动轨迹是线段OC,因为x=6,y=4,可得OC=4![]() .
.
解:(1)如图所示,若![]() ,
,
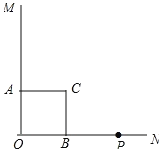
则![]() ,且
,且![]() ,
,
∴点![]() 到射线
到射线![]() 的距离为
的距离为![]() ;
;
(2)作![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
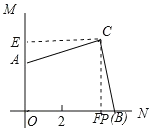
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
又∵![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]()
∴![]() ;
;
函数图象如图所示:
(3)连结![]() .
.
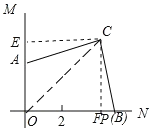
∵![]() ,
,
∴![]() 平分
平分![]() ,
,
∴点![]() 的运动轨迹是线段
的运动轨迹是线段![]() .
.
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴点![]() 运动过的路径长为
运动过的路径长为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目