题目内容
【题目】已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合. 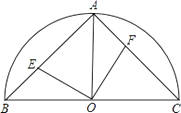
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x取值范围.
【答案】
(1)解:∵BC为半圆O的直径,OA为半径,且OA⊥BC,
∴∠B=∠OAF=45°,OA=OB,
又∵AE=CF,AB=AC,
∴BE=AF,
∴△BOE≌△AOF
∴S四边形AEOF=S△AOB= ![]() OBOA=2
OBOA=2
(2)解:∵BC为半圆O的直径,
∴∠BAC=90°,且AB=AC=2 ![]() ,
,
y=S△OEF=S四边形AEOF﹣S△AEF=2﹣ ![]() AEAF=2﹣
AEAF=2﹣ ![]() x(2
x(2 ![]() ﹣x)
﹣x)
∴y= ![]() x2﹣
x2﹣ ![]() x+2(0<x<2
x+2(0<x<2 ![]() )
)
【解析】(1)先根据BC为半圆O的直径,OA为半径,且OA⊥BC求出∠B=∠OAF=45°,再根据全等三角形的判定定理得出△BOE≌△AOF,再根据S四边形AEOF=S△AOB即可得出答案;(2)先根据圆周角定理求出∠BAC=90°,再根据y=S△OEF=S四边形AEOF﹣S△AEF即可得出答案.
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目