题目内容
【题目】问题：有甲、乙、丙三种商品，①购甲3件、乙5件、丙7件共需490元钱；②购甲4件、乙7件、丙10件共需690元钱；③购甲2件，乙3件，丙1件共需170元钱. 求购甲、乙、丙三种商品各一件共需多少元？
小明说：“可以根据3个条件列出三元一次方程组，分别求出购甲、乙、丙一件需多少钱，再相加即可求得答案.”
小丽经过一番思考后，说：“本题可以去掉条件③，只用①②两个条件，仍能求出答案.” 针对小丽的发言，同学们进行了热烈地讨论.
（1）请你按小明的思路解决问题.
（2）小丽的说法正确吗？如果正确，请完成解答过程；如果不正确，请说明理由.
（3）请根据上述解决问题中积累的经验，解决下面的问题：学校购买四种教学用具A、B、C、D，第一次购A教具1件、B教具3件、 C教具4件、D教具5件共花2018元；第二次购A教具1件、B教具5件、 C教具7件、D教具9件共花3036元. 求购A教具5件、B教具3件、 C教具2件、D教具1件共需多少元？
【答案】(1) 购甲、乙、丙三种商品各一件共需90元.(2) 小丽的说法正确. (3) 购A教具5件、B教具3件、 C教具2件、D教具1件共需3982元.
【解析】分析：（1）设购甲、乙、丙三种商品各一件分别需
元、
元、
元，根据题意列三元一次方程组求解即可；
（2）小丽的说法正确．设购甲、乙、丙三种商品各一件分别需元、元、元，根据题意列方程组，变形后用整体思想解答即可；
（3）设购买教学用具A、B、C、D各一件分别需
元、
元、
元、
元，根据题意列方程组，变形后用整体思想解答即可．
详解：（1）设购甲、乙、丙三种商品各一件分别需元、元、元，由题意得：
．
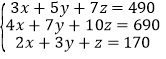解得：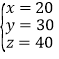 
．
∴ 
．
答：购甲、乙、丙三种商品各一件共需90元．
（2）小丽的说法正确．
设购甲、乙、丙三种商品各一件分别需元、元、元，由题意得：
．
变形得：
解得：①×3－②×2得：
∴x+y+z=90
答：购甲、乙、丙三种商品各一件共需90元．
（3）设购买教学用具A、B、C、D各一件分别需元、元、元、元，由题意得：
①×11－②×6得：
5a+3b+2c+d=3982
答：购A教具5件、B教具3件、 C教具2件、D教具1件共需3982元．
