题目内容
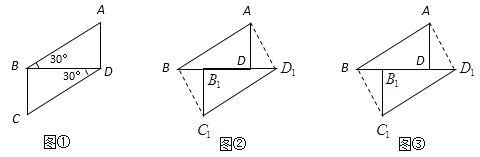
【题目】已知菱形![]() 的边长为
的边长为![]() ,
,![]() =120°,对角线
=120°,对角线![]() 相交于点
相交于点![]() ,以点
,以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴、
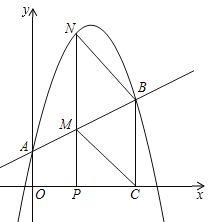
轴、![]() 轴,建立如图所示的直角坐标系,以
轴,建立如图所示的直角坐标系,以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
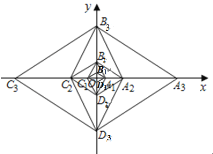
菱形![]() ,…,按此规律继续做下去,设菱形
,…,按此规律继续做下去,设菱形![]() 的面积为
的面积为![]() ,菱形
,菱形![]() 的面积为
的面积为![]() ,…,菱形
,…,菱形![]() 的面积为
的面积为![]() ,则
,则![]() _____.
_____.
【答案】![]()
【解析】
先根据菱形的性质及锐角三角函数的定义求出OA1,OB1的长,从而可求出S1,根据相似及锐角三角函数的定义可求得OA2,OB2的长,从而可得出S2,…,找出规律即可得出结论.
解:∵菱形A1B1C1D1的边长为2,∠A1B1C1=120°,
∴∠A1B1O=60°,∠A1OC1=90°,
∴OA1=A1B1sin60°=2×![]() =
=![]() ,OB1=A1B1cos60°=2×
,OB1=A1B1cos60°=2×![]() 1,
1,
∴A1C1=2OA1=2![]() ,B1D1=2OB1=2,
,B1D1=2OB1=2,
∴S1=![]() ×A1C1×B1D1=
×A1C1×B1D1=![]() .
.
∵菱形A1B1C1D1∽菱形B2C1D2A1∽菱形![]() ,
,
∴∠A2B2C2=∠B2A1D2=∠A1B1C1=120°,
∴OB2=![]() ,
,
∴OA2=OB2×tan60°=3![]() ,B2D2=2OB2=6,
,B2D2=2OB2=6,
∴A2C2=2OA2=6![]() ,
,
∴S2=![]() ×A2C2×B2D2=
×A2C2×B2D2=![]() =2
=2![]() ×9,
×9,
同理可得,
S3=![]() ×A3C3×B3D3=
×A3C3×B3D3=![]() ,
,
S4=![]() ×A4C4×B4D4=
×A4C4×B4D4=![]() ,
,
…
∴Sn=![]() .
.
故答案为:![]() .
.

【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.