��Ŀ����
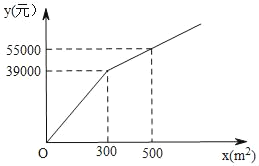
����Ŀ���������ƻ���һ������¥����Ϊ������ʵ���л�������䣬������Ҫ�����������̣����ڿ�����������¥֮����һ���߿Ƽ��ĵ�·���ڶ���¥���з����䴦������֪�������y��Ԫ�������������¥�ľ���xkm֮��Ĺ�ϵʽΪy��ax+b(0��x��3)����������������¥�ľ���Ϊ1kmʱ�����������Ϊ720��Ԫ��������������¥�ľ���Ϊ3km�����3kmʱ������Ӱ����Բ��ƣ������з����䴦��������·�ķ�����x2�����ȣ��ұ���ϵ��Ϊm��Ԫ�������̷�w���������+��·�ѣ�
(1)��������������¥�ľ���x��3kmʱ���������y��____��Ԫ��a��____��b��____��
(2)��m��90ʱ��������������¥�ľ���Ϊ����kmʱ�������̷����٣�
(3)�����������̷Ѳ�����675��Ԫ���ҿ���������¥�ľ���С�ڵ���3km����m�ķ�Χ��
���𰸡�(1)0����360��1080��(2)������Ϊ2����ʱ�������̷������٣�(3)0��m��80��
��������
(1)��x��1ʱ��y��720����x��3ʱ��y��0����x��y����y��ax+b��������⣻
(2)������Ŀ�������̷�w���������+��·�ѷ�0��x��3��x��3ʱ����.
����0��x��3ʱ�������̷�W��90x2��360x+1080������x��3ʱ��W��90x2���ֱ�����Сֵ���ɣ�
(3)0��x��3��W��mx2��360x+1080��(m��0)����Գ���x��![]() ��Ȼ�����ۣ�x��
��Ȼ�����ۣ�x��![]() =3ʱ��x��
=3ʱ��x��![]() ��3ʱ�������mȡֵ������⣮
��3ʱ�������mȡֵ������⣮
�⣺(1)��x��1ʱ��y��720����x��3ʱ��y��0����x��y����y��ax+b��
��ã�a����360��b��1080��
�ʴ�Ϊ��0����360��1080��
(2)����0��x��3ʱ�������̷�W��90x2��360x+1080��
����x��2ʱ��Wmin��720��
����x��3ʱ��W��90x2��
W��x�������
��x��3ʱ��Wmin��810��720��
��������Ϊ2����ʱ�������̷������٣�
(3)��0��x��3��
W��mx2��360x+1080��(m��0)����Գ���x��![]() ��
��
��x��![]() ��3ʱ������m��60��
��3ʱ������m��60��
Wmin��m(![]() )2��360(
)2��360(![]() )+1080��
)+1080��
��Wmin��675����ã�60��m��80��
��x��![]() ��3ʱ����m��60��
��3ʱ����m��60��
��x��3ʱ��Wmin��9m��675��
��ã�0��m��60��
�ʣ�0��m��80��

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�