题目内容
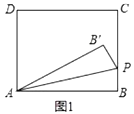
【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 ,点H对应的数轴上的数是 ;
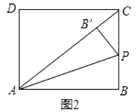
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.

【答案】(1)-5,-1(2)![]() ɑ+22.5°(3)∠M+∠N=97.5°.
ɑ+22.5°(3)∠M+∠N=97.5°.
【解析】(1)-5,-1
(2) ∵∠AHF的平分线和∠AGH的平分线交于点M,
∴∠FHM=![]() ∠FHA,∠HGM=
∠FHA,∠HGM=![]() ∠HGA,
∠HGA,
∵∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,
∴2∠M+2∠HGM=∠HGA+∠HAG,
∴∠M=![]() ∠HAG=
∠HAG=![]() (∠HAO+∠OAG)=
(∠HAO+∠OAG)=![]() ɑ+22.5°
ɑ+22.5°
(3) ∵∠EFH的平分线和∠FOC的平分线交于点N,
∴∠N=90°-![]() ∠FAO=90°-
∠FAO=90°-![]() ∠FAH-
∠FAH-![]() ∠OAH (可以直接利用∠N=90°-
∠OAH (可以直接利用∠N=90°-![]() ∠FAO)
∠FAO)
=90°-15°-![]() ∠OAH
∠OAH
=75°-![]() ∠OAH,
∠OAH,
∵∠M=![]() ∠OAH+22.5°,
∠OAH+22.5°,
∴∠M+∠N=97.5°.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.