题目内容
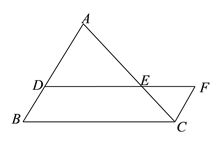
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE、OE.
(1)求证:DE是⊙O的切线;
(2)填空:
①当∠CAB= 时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .

【答案】(1)证明见解析(2)①45°②正方形
【解析】【试题分析】(1)连接BD,根据直径所对的圆周角是直角,得![]() ,因为E为BC边的中点,根据直角三角形斜边上的中线等于斜边的一半,得ED=EB,根据等边对等角,得∠EDB=∠EBD,由于OD=OB,得∠ODB=∠OBD.因为∠EBD+∠OBD=90°,所以∠EDB+∠ODB=90°,根据切线的定义得:DE是⊙O的切线.
,因为E为BC边的中点,根据直角三角形斜边上的中线等于斜边的一半,得ED=EB,根据等边对等角,得∠EDB=∠EBD,由于OD=OB,得∠ODB=∠OBD.因为∠EBD+∠OBD=90°,所以∠EDB+∠ODB=90°,根据切线的定义得:DE是⊙O的切线.
(2)①因为E为BC边的中点,O为AB边的中点, ![]() , 欲使四边形AOED是平行四边形,则
, 欲使四边形AOED是平行四边形,则![]() ,即D为AC边的中点,又因为
,即D为AC边的中点,又因为![]() ,则Rt△ABC为等腰直角三角形.即∠CAB=45
,则Rt△ABC为等腰直角三角形.即∠CAB=45![]() ;②
;②![]() 则四边形OBED是平行四边形,因为
则四边形OBED是平行四边形,因为![]() ,则平行四边形OBED为矩形,因为OB=BE,得矩形OBED为正方形.
,则平行四边形OBED为矩形,因为OB=BE,得矩形OBED为正方形.
【试题解析】
(1)连接OD、BD,
∴∠ADB=∠BDC=90°.
∵在Rt△BDC中,E为BC边的中点,
∴ED=EB=![]() BC.
BC.
∴∠EDB=∠EBD.
∵OD=OB,
∴∠ODB=∠OBD.
在Rt△ABC中,∠ABC=90°,
即∠EBD+∠OBD=90°,
∴∠EDB+∠ODB=90°,即∠ODE=90°.
∴DE是⊙O的切线.
(2)①因为E为BC边的中点,O为AB边的中点, ![]() ,
,
欲使四边形AOED是平行四边形,则![]() ,即D为AC边的中点,因为
,即D为AC边的中点,因为![]() ,则Rt△ABC为等腰直角三角形.即∠CAB=45
,则Rt△ABC为等腰直角三角形.即∠CAB=45![]() ;
;
②![]() 则四边形OBED是平行四边形,因为
则四边形OBED是平行四边形,因为![]() ,则平行四边形OBED为矩形,又因为OB=BE,得矩形OBED为正方形.
,则平行四边形OBED为矩形,又因为OB=BE,得矩形OBED为正方形.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案