Question

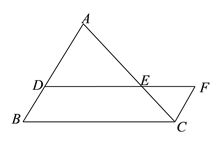
【题目】如图，已知△ABC中，点D、E分别在边AB和AC上，DE∥BC，点F是DE延长线上的点， ，联结FC，

（1）求证：AB//CF；

（2）若，FC=6，求AB的长．

Answer 1

【答案】见解析

【解析】试题分析:(1) 因为DE∥BC,根据平线分线段成比例可证得, ,因为,

所以,又因为∠AED=∠CEF,可证△AED∽△CEF,可证得: ∠ADE=∠F,利用内错角相等两直线平行可判定,（2）因为DE∥BC, AB//CF,可判定四边形BDFC是平行四边形,所以FC=BD,根据△AED∽△CEF,可得,根据可得: ,即,因为FC=6,所以AD=12,所以AB=18.

解：（1）∵,

∴,

∵,

∴,

∴AB//CF ,

（2）∵DE∥BC,AB//CF,

∴四边形DBCF是平行四边形,

∴BD=CF=6,

∵AB//CF,

∴,

∴AD=12,

∴AB=18,

或：先证明△FCE∽△ABC,得，得,

所以AB=18 .