题目内容
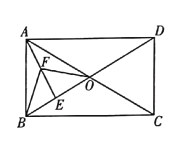
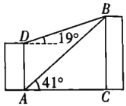
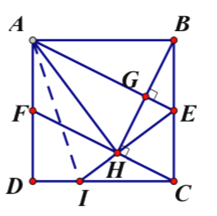
【题目】如图1，正方形
中， 点
是
的中点，过点
作
于点
，过点
作
垂直
的延长线于点
，交
于点
．
（1）求证：
；
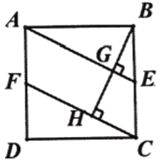
（2）如图2，连接
，连接
并延长交
于点I，
①求证：
；
②求
的值．
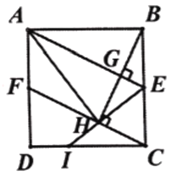
【答案】（1）证明见解析；（2）①证明见解析；②
【解析】
（1）根据正方形的性质与已知条件证明
，利用AAS证明
；
（2）①结合（1）证明
，根据相似三角形的性质进行求证；
②方法一：延长
和
交于点
，由正方形的性质与已知条件得出四边形
是平行四边形，
，
，由①得出
，进而可求出
，最后根据相似三角形的性质进行求解；
方法二：连接
，利用直角三角形斜边上的中线为斜边的一半得出
，进而证明
，
，根据全等三角形的性质得出
，设
，
， 在
中利用勾股定理求出x，进而求解．
解：（1）证明：
四边形
是正方形，
，
，
，
，
的延长线于点
，交于点
，
，
，
，
（AAS）；
（2）①证明：
，
又
，
即
，
，
，
，
；
②方法一：如图，延长和交于点，
，的延长线于点，交于点，
，
四边形是正方形，
，
四边形是平行四边形，，，
，
点
是
中点，
在
中，
，
，
，
点是中点，
，
，
，
，
，
，
，
，
；
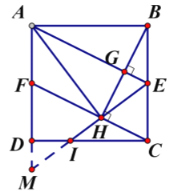
方法二：如图， 连接，
点是中点，
，
，
，
，
，
，
，
又
，
，
，
，
，
，
，
设，，则
，
，
在中，由勾股定理得，
解得，
，
，
．
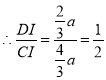【题目】为庆祝建国70周年，某校举办了爱我中华知识竞赛活动．该校南、北两个校区七年级各有300名学生参加竞赛活动．为了解这两个校区参赛学生成绩情况，从中各随机抽取了10名学生的成绩进行调查，过程如下：
（收集、整理、描述数据）根据随机抽取的10名学生的成绩，制作了如下统计图表：
（说明：成绩90分及以上为优秀，80-89分为良好，60-79分为合格，60分以下为不合格）
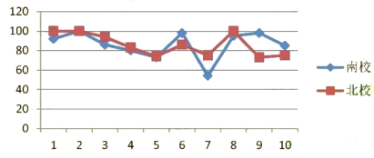
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
（分析数据）对上述数据进行分析，分别求出了两组样本数据的平均数、中位数、众数如下表：
校区 | 平均数（分） | 中位数（分） | 众数（分） |
南校 | 87 | 90．5 | |
北校 | 86 | 100 |
（得出结论）综合上述统计全过程，回答下列问题：
（1）补全表格．
（2）估计北校七年级学生竞赛成绩为优秀的人数．
（3）你认为哪个校区的七年级学生竞赛成绩比较好？说明你的理由．（从两个不同的角度说明推断的合理性）
【题目】我市某校组织“学经典，用经典”知识竞赛，每班参加比赛的学生人数相同，成绩分为
四个等级，其中相应等级的得分依次记为
分，
分，
分，
分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：
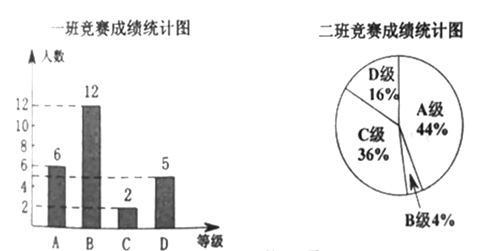
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班成绩“
级”的人数为 ；
（2）请你将下表补充完整：
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
（3）请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)
