题目内容
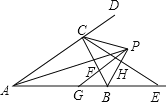
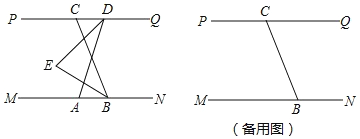
【题目】如图,已知 MN∥PQ,B 在 MN 上,C 在 PQ 上,A 在 B 的左侧,D 在 C 的右侧,DE 平分∠ADC,BE平分∠ABC,直线 DE,BE 交于点 E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED 的度数;
(2)将线段 AD 沿 DC 方向平移,使得点 D 在点 C 的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含 n 的代数式表示)
【答案】(1)65°;(2)∠BED=210°﹣(![]() n)°或(
n)°或(![]() n)°﹣30°或 30°﹣(
n)°﹣30°或 30°﹣(![]() n)°.
n)°.
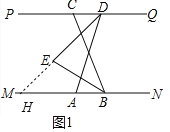
【解析】(1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分三种情形讨论即可解决问题.
(1)如图 1 中,延长 DE 交 MN 于 H.
∵∠ADQ=110°,ED 平分∠ADP,
∴∠PDH=![]() ∠PDA=35°,
∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB 平分∠ABC,
∴∠EBH=![]() ∠ABC=30°,
∠ABC=30°,
∴∠BED=∠EHB+∠EBH=65°.
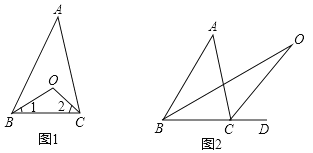
(2)有 3 种情形,如图 2 中,当点 E 在直线 MN 与直线 PQ 之间时.延长 DE 交 MN 于 H.
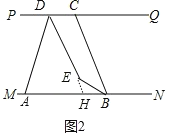
∵PQ∥MN,
∴∠QDH=∠DHA=![]() n°,
n°,
∴∠BED=∠EHB+∠EBH=180°﹣(![]() n)°+30°=210°﹣(
n)°+30°=210°﹣(![]() n)°,
n)°,
当点 E 在直线 MN 的下方时,如图 3 中,
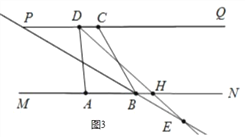
设 DE 交 MN 于 H.
∵∠PBC=∠ABP=30°,
∴∠HBE=∠ABP=30°(对顶角).
∵∠ADH=∠CDH=(![]() n)°,
n)°,
∴∠CDH=∠DHB=(![]() n)°(两直线平行,内错角相等).
n)°(两直线平行,内错角相等).
又∵∠DHB=∠HBE+∠HEB,
∴∠BED=(![]() n)°﹣30°,
n)°﹣30°,
当点 E 在 PQ 上方时,如图 4 中,
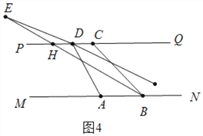
设 PQ 交 BE 于 H.同法可得∠BED=30°﹣(![]() n)°.
n)°.
综上所述,∠BED=210°﹣(![]() n)°或(
n)°或(![]() n)°﹣30°或 30°﹣(
n)°﹣30°或 30°﹣(![]() n)°.
n)°.

 阅读快车系列答案
阅读快车系列答案