题目内容
如图，矩形ABCD两邻边分别为3、4，点P是矩形一边上任意一点，则点P到两条对角线AC、BD的距离之和PE+PF为_____________.
12/5
设PE=x，PF=a，PB=y．
由∠PBF=∠ABD，∠PFB=∠DAB可得△ABD∽△FBP，
故a/4=y/5,
同理可证x/4=(3-y)/5,
故a+x=4/5×3=12/5
故答案为12/5
由∠PBF=∠ABD，∠PFB=∠DAB可得△ABD∽△FBP，
故a/4=y/5,
同理可证x/4=(3-y)/5,
故a+x=4/5×3=12/5
故答案为12/5
练习册系列答案
阅读快车系列答案
相关题目
中，
，对角线
平分
，则梯形
如不能成功，请说明理由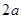
，沿图中线段DE、CF将△ABC剪开，分成的三块图形恰能拼成正方形CFHG，如图1所示．请你解决如下问题：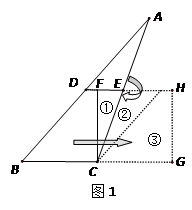
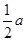．请你设计两种不同的分割方法，将△A′B′C′沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图2、图3中，画出分割线及拼接后的图形．
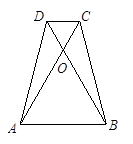
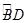，M是BC的中点，过点M作EM⊥BC交
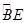的长为 ★ ．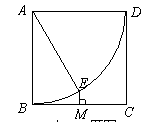
，求证四边形DEBF是菱形．