Question

【题目】某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，如果每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球从发射出到第一次落在桌面的运行过程中，设乒乓球与端点A的水平距离为x（米），距桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：

t（秒）	0	0.16	0.2	0.4	0.6	0.64	0.8	…
x（米）	0	0.4	0.5	1	1.5	1.6	2	…
y（米）	0.25	0.378	0.4	0.45	0.4	0.378	0.25	…

（1）如果y是t的函数，

①如图，在平面直角坐标系tOy中，描出了上表中y与t各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；

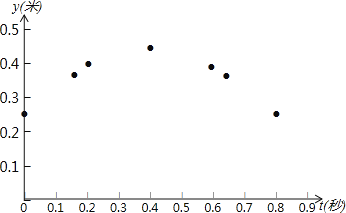
②当t为何值时，乒乓球达到最大高度？

（2）如果y是关于x的二次函数，那么乒乓球第一次落在桌面时，与端点A的水平距离是多少？

Answer 1

【答案】（1）①见解析；②t=0.4（秒），乒乓球达到最大高度；（2）m．

【解析】

试题分析：（1）①根据描出了上表中y与t各对对应值为坐标的点，画出该函数的图象即可；

②利用网格中数据直接得出乒乓球达到最大高度时的时间；

（2）首先求出函数解析式，进而求出乒乓球落在桌面时，与端点A的水平距离．

解：（1）①如图所示，

②由表格中数据可得，t=0.4（秒），乒乓球达到最大高度；

（2）由表格中数据，可设y=a（x﹣1）2+0.45，

将（0，0.25）代入，可得：a=﹣，

则y=﹣（x﹣1）2+0.45，

当y=0时，0=﹣（x﹣1）2+0.45，

解得：x1=，x2=﹣（舍去），

即乒乓球与端点A的水平距离是m．