题目内容
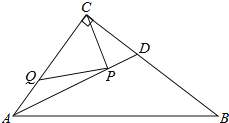
【题目】如图，在
中，
，
，
，AD是
的平分线．若P，Q分别是AD和AC上的动点，则
的最小值是（ ）
A.
B.4C.5D.
【答案】D
【解析】
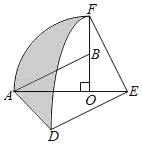
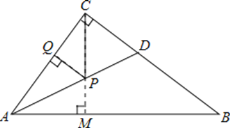
过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，由AD是∠BAC的平分线．得出PQ=PM，这时PC+PQ有最小值，即CM的长度，运用勾股定理求出AB，再运用S△ABC=
ABCM=ACBC，得出CM的值，即PC+PQ的最小值．
如图，过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，
∵AD是∠BAC的平分线．
∴PQ=PM，这时PC+PQ有最小值，即CM的长度，
∵AC=6，BC=8，∠ACB=90°，
∴AB=
=10．
∵S△ABC=ABCM=ACBC，
∴CM=
，
即PC+PQ的最小值为
．
故选：D．
练习册系列答案
相关题目
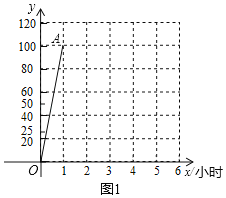
【题目】研究表明：人对事物的认识分成记忆和遗忘两个阶段，即强化记忆至记忆量为100；然后停止强化记忆，开始遗忘．如图1中的线段OA是小明在1小时之内对某篇文章进行强化记忆时小明的记忆量y与时间x小时之间的函效图象；当小明停止强化记忆后，记忆量y与时间x小时的变化情况如下表（图2）所示：
（1）把图2所示的表中（x，y）的各组对应值作为点的坐标，在如图1所示的平面直角坐标系中描出各点，并用一条平滑的曲线顺次连接，观察所画的图象，猜测小明停止强化记忆后是关于x的什么函数，并求出该函数解析式．
（2）研究表明：当记忆量在75以上（含75）时，称为熟记．请问：小明共有多少分钟对一篇文章维持熟记程度？
从开始记忆所经历的时间x/小时 | 1 | 2 | 3 | 4 |
学生的记忆量y | 100 | 50 | 25 | 20 |
