��Ŀ����
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC��3cm����B��30������D��BC������C��B�����˶���D����B��C�غϣ��������˶��ٶ�Ϊ1cm/s������AD������ADE��30����DE���߶�AC�ڵ�E��
��1���ڴ��˶������У���BDA���� �������С������D���˶���ͼ1λ��ʱ����BDA��75�������BAD���� ����
��2����D�˶�3s��ͼ2λ�ã���CD���� ������ʱ��ABD�͡�DCE�Ƿ�ȫ�ȣ���˵�����ɣ�
��3���ڵ�D�˶������У���ADE����״Ҳ�ڱ仯���жϵ���ADE�ǵ���������ʱ����BDA���ڶ��ٶȣ���ֱ��д�������

���𰸡���1����75������2��3cm����ABD�͡�DCEȫ�ȣ����ɼ���������3��105��� 60��
��������
��1�����ݵ�D���˶�����жϡ�BDA�ı仯��������ݵ��������ε����ʡ��������ڽǺͶ��������BAD��
��2�����ݵ�D���˶�������CD������ASA����֤����ABD�ա�DCE��
��3����AD=AE��DA=DE��EA=ED������������ݵ��������ε����ʽ�Ͻǵļ��������BDA�Ķ�����
�⣺��1���ڴ��˶������У���BDA���
D���˶���ͼ1λ��ʱ����BAD=180��-��B-��BDA=75����
�ʴ�Ϊ����75����
��2����D�˶�3s��ͼ2λ�ã�CD=3cm����ʱ��ABD�ա�DCE��
�������£���AB=AC����B=30����
���C=30����
��CD=CA=3cm��
���CAD=��CDA=![]() ����180��-30����=75����
����180��-30����=75����
���ADB=105������EDC=75��-30��=45����
���DEC=180��-45��-30��=105����
���ADB=��DEC��
����ABD����DCE��
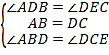 ��
��
���ABD�ա�DCE��ASA����
��3����ADE������������������
�ٵ�AD=AEʱ����ADE=30����
���AED=��ADE=30������DAE=180��-��ADE-��AED=120����
�ߡ�BAC=180��-��B-��C=120����D����B��C�غϣ�
��AD��AE��
�ڵ�DA=DEʱ����ADE=30����
���DAE=��DEA=![]() ��180��-��ADE��=75����
��180��-��ADE��=75����
���BDA=��DEC=180��-��AED=105����
�۵�EA=EDʱ����ADE=30����
���EAD=��EDA=30����
���AED=180��-��EAD-��EDA=120����
���BDA=��DEC=180��-��AED=60����
���Ͽ�֪���ڵ�D���˶������У���ADE����״�����ǵ��������Σ���ʱ��BDA�Ķ���Ϊ60����105����





