题目内容
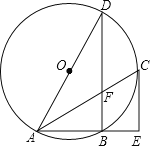
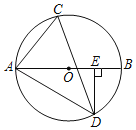
【题目】如图,AB是⊙O的直径,D是⊙O上一点,DE⊥AB于点E,且∠ADE=60°,C是![]() 上一点,连结AC,CD.
上一点,连结AC,CD.
(1)求∠ACD的度数;
(2)证明:AD2=ABAE;
(3)如果AB=8,∠ADC=45°,请你编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
【答案】(1)∠ACD=60°;(2)见解析;(3)请计算AC的长度,AC=4![]() .
.
【解析】
(1)连接OD,利用圆周角定理和等腰三角形的性质解答;
(2)连接BD,利用圆周角定理和射影定理证明或通过证明△ADE∽△ABD得到该结论;
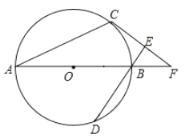
(3)求AC的长度.如图2,连接OC,BC,利用圆周角定理和等腰三角形的判定得到△ABC是等腰直角三角形,则由勾股定理了求得AC的长度即可.
(1)如图,连接OD,
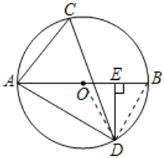
∵OA=OD,∠ADE=60°,DE⊥AB,
∴∠OAD=∠ODA=90°-∠ADE =90°-60°=30°.
∴∠AOD=180°-∠OAD-∠ODA=180°-30°-30° =120°,
∴∠ACD=![]() ∠AOD=60°;
∠AOD=60°;
(2)如图,连接BD,

∵AB是⊙O的直径,
∴∠ADB=90![]() ,
,
∵在△ADE和△ABD中,∠DAE=∠BAD,∠AED=∠ADB=90![]() ,
,
∴△ADE∽△ABD.
∴![]() .
.
∴AD2=AB![]() AE;
AE;
(3)请计算AC的长度.
如图2,连接OC,BC.
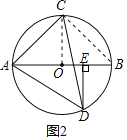
∵∠ADC=45°,
∴∠AOC=2∠ADC=90°,
又∵点O是AB的中点,
∴AC=BC,
又∵AB是直径,
∴∠ACB=90°,
∴AC2+BC2=AB2,即2AC2=AB2=82,
则AC=4![]() .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目