题目内容
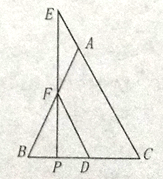
【题目】如图,在ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.
【答案】见解析
【解析】试题分析:
由已知条件易证△BDF是等腰三角形,结合FP⊥BD可得∠DFP=∠BFP=∠AFE;再由DF∥AC可得∠E=∠DFP,从而可得∠AFE=∠E,即可得到AE=AF.
试题解析:
∵FD∥AC,
∴∠PFD=∠E,∠FDB=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B,
∴FB=FD.
又∵EP⊥BC,
∴∠PFB=∠PFD,
∵∠PFB=∠AFE,
∴∠PFD=∠AFE,
又∵∠PFD=∠E,
∴∠E=∠AFE,
∴AE=AF,即△AEF是等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目