Question

【题目】如图，在平面直角坐标系内，已知点A（2，2），B（﹣6，﹣4），C（2，﹣4）．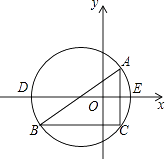
（1）求△ABC的外接圆的圆心点M的坐标；
（2）求△ABC的外接圆在x轴上所截弦DE的长．

Answer 1

【答案】
（1）解：∵B（﹣6，﹣4），C（2，﹣4），

∴线段BC的垂直平分线是x=﹣2，

∵A（2，2），C（2，﹣4），

∴线段AC的垂直平分线是y=﹣1，

∴△ABC的外接圆的圆心M的坐标为：（﹣2，﹣1）

（2）解：连接OM，作MN⊥DE于N，

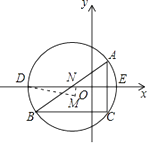
由题意得，AC=6，BC=8，

由勾股定理得，AB=10，

则DN= =2 ，

由垂径定理得，DE=2DN=4 ．

【解析】（1）根据三角形的外心是三角形三边垂直平分线的交点解答；（2）连接OM，作MN⊥DE于N，根据勾股定理求出DN，根据垂径定理求出DE．