��Ŀ����
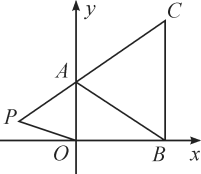
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��0��a����B��b��0����C��b��c�����㣬����a��b��c�����ϵʽ![]() ����b��3��2��0����c��4��2��0.
����b��3��2��0����c��4��2��0.
��1����a��b��c��ֵ��
��2�����������ABC�������
��3������ڵڶ���������һ��P��m��![]() ������ô���ú�m��ʽ�ӱ�ʾ�ı���ABOP�������
������ô���ú�m��ʽ�ӱ�ʾ�ı���ABOP�������
��4���ڣ�3���������£��Ƿ���ڵ�P��ʹ�ı���ABOP�������������ABC�������ȣ������ڣ������P�����ꣻ�������ڣ���˵������.
���𰸡���1��a=2��b=3��c=4����2��S��ABC =6����3��S�ı���ABOP =3+m����4��P��-3��![]() ��
��
��������
��1���÷Ǹ�����������⣻
��2����BC���������֪BCƽ��y�ᣬ���ɵ���ABC=![]() .
.
��3�����ı���ABOP�����������������������ͣ���m����ʾ��
��4����ABC��������֪�����������⣬���̼��ɣ�
�⣺��1������֪![]() ����b��3��2��0����c-4��2��0��
����b��3��2��0����c-4��2��0��
��a-2=0��b-3=0��c-4=0.
�ɵã�a=2��b=3��c=4��
��2����B��3��0��C��3��4��
��BC=4��
��S��ABC=![]() ��4��3=6
��4��3=6
��3����S��ABO=![]() ��2��3=3��S��APO=
��2��3=3��S��APO=![]() ��2��m=m��
��2��m=m��
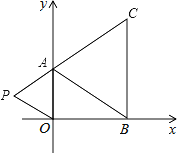
��S�ı���ABOP=S��ABO+S��APO=3+m=3+m
��4����ΪS��ABC=![]() ��4��3=6��
��4��3=6��
��S�ı���ABOP=S��ABC
��3+m=6��
�� m=3��
���Դ��ڵ�P��-3��![]() ��ʹS�ı���ABOP=S��ABC��
��ʹS�ı���ABOP=S��ABC��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�