题目内容
【题目】已知:在正方形![]() 中,点
中,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,
,
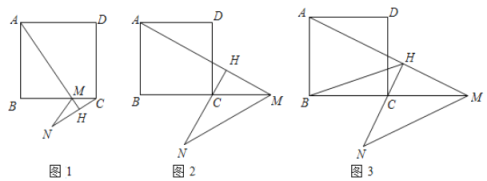
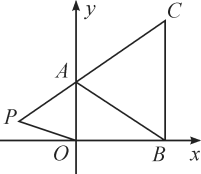
(1)如图1,当点![]() 在
在![]() 边上,求证:
边上,求证:![]() ;
;
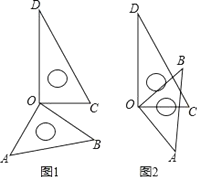
(2)如图2,当点![]() 在
在![]() 的延长线上,求证:
的延长线上,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)BH=![]() .
.
【解析】
(1)利用平行线的性质以及三角形的外角的性质证明即可.
(2)如图2中,延长MN,AB交于点K,连接CK,只要证明△AMB≌△KMB(ASA),CN=KN即可解决问题.
(3)如图(3)中,延长MN,AB交于点K,连接CK,CA,BN,AC,延长AC交KM于E,作HF⊥BM于F.想办法证明BC=CM,推出tan∠AMB=tan∠BMK=![]() ,解直角三角形求出HF,BF即可解决问题.
,解直角三角形求出HF,BF即可解决问题.
(1)证明:如图1中,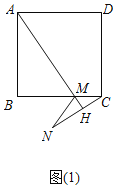
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAH=∠AMB,
∵∠AMB=∠NMB,∠NMB=∠N+∠NCB,
∴∠DAH=∠N+∠NCB.
(2)证明:如图2中,延长MN,AB交于点K,连接CK,CA.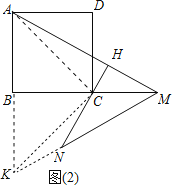
在正方形ABCD中,∠ABC=90°,AD∥BC,
∵∠AMB=∠BMN,
∵∠ABM=∠KBM=90°,BM=BM,
∴△AMB≌△KMB(ASA),
∴BK=AB=BC,∠BKM=∠BAM,AM=KM,
∴∠BKC=∠BCK,
∵CH⊥AM,
∴∠BAM=90°-∠AMB=90°-∠CMH=∠BCN,
∴∠BKM=∠BCN,
∴∠BKC-∠BKM=∠BCK-∠BCN,
∴∠NKC=∠NCK,
∴NK=NC,
∵KM=MN+NK,
∴AM=MN+CN.
(3)解:如图(3)中,延长MN,AB交于点K,连接CK,CA,BN,AC,延长AC交KM于E,作HF⊥BM于F.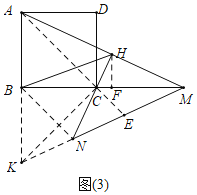
设CN=KN=x,则MN=2x,
∵BK=BC,BN=BN,KN=KC,
∴△BNK≌△BNC(SSS),
∴∠NBK=∠NBC=![]() ∠CBK=45°,
∠CBK=45°,
∵四边形ABC都是正方形,
∴∠BAC=45°,
∴∠NBK=∠BAC,
∴AE∥BN,
∵AB=BK,
∴KN=NE=x,
∴EN=EM=x,
∵CE∥BN,EN=EM,
∴BC=CM,
∴tan∠AMB=tan∠BMK=![]() =
=![]() ,
,
在Rt△CHM中,∵∠CHM=90°,
∴tan∠CMH=![]() ,
,
∵CH=2![]() ,
,
∴MH=4![]() ,
,
∴CM=![]() =10,
=10,
∵![]() CHHM=
CHHM=![]() CMHF,
CMHF,
∴FH=4,FM=8,CF=2,
在Rt△BHF中,BH=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
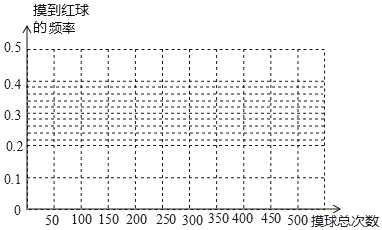
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).