题目内容
已知边长为5的等边三角ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC，则CE的长是________．
20-10
分析：先根据题意画出图形，由等边三角形的性质可知∠C=60°，设CE=x，则AE=5-x，由图形翻折变换的性质可知，AE=ED=5-x，再根据ED⊥BC，∠C=60°可求出∠CED=30°，故CD=
CE，再在Rt△CDE中利用勾股定理即可求出x的值．
解答：
解：如图所示：
∵△ABC是等边三角形，AB=5，
∴∠C=60°，
设CE=x，则AE=5-x，
∵△DEF是△AEF翻折而成，
∴AE=DE=5-x，
∵ED⊥BC，∠C=60°，
∴∠CED=30°，
∴CD=CE=
，
在Rt△CDE中，∠CED=30°，CD=，DE=5-x，
∴tan∠CED=tan30°=
=
，
即=
，
解得，x=20-10．
故答案为：20-10．
点评：本题考查的是图形翻折变换的性质、等边三角形的性质、直角三角形的性质，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．
分析：先根据题意画出图形，由等边三角形的性质可知∠C=60°，设CE=x，则AE=5-x，由图形翻折变换的性质可知，AE=ED=5-x，再根据ED⊥BC，∠C=60°可求出∠CED=30°，故CD=
CE，再在Rt△CDE中利用勾股定理即可求出x的值．解答：
解：如图所示：∵△ABC是等边三角形，AB=5，
∴∠C=60°，
设CE=x，则AE=5-x，
∵△DEF是△AEF翻折而成，
∴AE=DE=5-x，
∵ED⊥BC，∠C=60°，
∴∠CED=30°，
∴CD=
CE=，在Rt△CDE中，∠CED=30°，CD=
，DE=5-x，∴tan∠CED=tan30°=
=，即
=，解得，x=20-10
．故答案为：20-10
．点评：本题考查的是图形翻折变换的性质、等边三角形的性质、直角三角形的性质，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
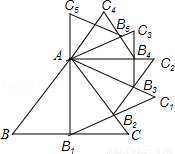
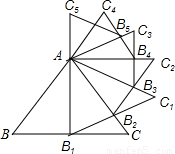
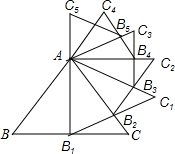（2013•黑龙江）已知等边三角形ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边三角形AB1C1，再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边三角形AB2C2，再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形，得到第三个等边AB3C3；…，如此下去，这样得到的第n个等边三角形ABnCn的面积为
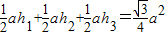，可得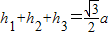
．