题目内容
(2012•南湖区二模)在特殊四边形的复习课上,王老师出了这样一道题:
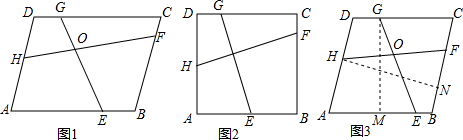
如图1,在?ABCD中,E、F、G、H分别为AB,BC,CD,DA边上的动点,连接EG,HF相交于点O,且∠HOE=∠ADC,若AB=a,AD=b,试探究:EG与FH的数量关系.
经过小组讨论后,小聪建议分以下三步进行,请你解答:
(1)特殊情况,探索结论
当?ABCD是边长为a的正方形时(如图2),请写出EG与FH的数量关系(不必证明);
(2)尝试变题,再探思路
当?ABCD是边长为a的菱形时(如图3),EG与FH又有怎样的数量关系呢?
小聪想:要求EG与FH的数量关系,就要构成全等三角形或相似三角形,于是,分别过点G、H作GM⊥AB于点M,HN⊥BC于点N,在△HNF和△GME中,有∠GME=∠HNF=Rt∠,由菱形面积与性质可得GM=HN,能否从已知条件得到∠MGE=∠NHF呢?请你根据小聪的思路完成解答过程;
(3)特例启发,解答题目
猜想:原题中EG与FH的数量关系是
=
=
,并说明理由.
如图1,在?ABCD中,E、F、G、H分别为AB,BC,CD,DA边上的动点,连接EG,HF相交于点O,且∠HOE=∠ADC,若AB=a,AD=b,试探究:EG与FH的数量关系.
经过小组讨论后,小聪建议分以下三步进行,请你解答:
(1)特殊情况,探索结论
当?ABCD是边长为a的正方形时(如图2),请写出EG与FH的数量关系(不必证明);
(2)尝试变题,再探思路
当?ABCD是边长为a的菱形时(如图3),EG与FH又有怎样的数量关系呢?
小聪想:要求EG与FH的数量关系,就要构成全等三角形或相似三角形,于是,分别过点G、H作GM⊥AB于点M,HN⊥BC于点N,在△HNF和△GME中,有∠GME=∠HNF=Rt∠,由菱形面积与性质可得GM=HN,能否从已知条件得到∠MGE=∠NHF呢?请你根据小聪的思路完成解答过程;
(3)特例启发,解答题目
猜想:原题中EG与FH的数量关系是
| EG |
| FH |
| b |
| a |
| EG |
| FH |
| b |
| a |

分析:(1)过G作GM⊥AB于M,过H作HN⊥BC于N,求出GM=HN,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME≌△HNF即可;
(2)过G作GM⊥AB于M,过H作HN⊥BC于N,根据菱形面积公式求出GM=HN,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME≌△HNF即可;
(3)过G作GM⊥AB于M,过H作HN⊥BC于N,根据平行四边形面积公式求出
=
=
,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME∽△HNF即可.
(2)过G作GM⊥AB于M,过H作HN⊥BC于N,根据菱形面积公式求出GM=HN,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME≌△HNF即可;
(3)过G作GM⊥AB于M,过H作HN⊥BC于N,根据平行四边形面积公式求出
| GM |
| HN |
| BC |
| AB |
| b |
| a |
解答:(1)解:EG=FH,
理由是: 过G作GM⊥AB于M,过H作HN⊥BC于N,
过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是正方形,
∴DC=AB,AD∥BC,DC∥AB,AD=BC,∠D=∠A=∠B=∠C=90°,
∴GM∥AD∥BC,HN∥DC∥AB,
∴四边形ADGM、四边形GMBC、四边形AHNB,四边形DCNH是平行四边形,
∴DC=HN=AB,AD=GM=BC,
∴HN=GM,
∵∠ADC=∠HOE=90°,
∴∠DHO+∠DGE=360°-90°-90°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∵HN⊥BC,GM⊥AB,
∴∠GME=∠HNF=90°,
在△GME和△HNF中
∴△GME≌△HNF(AAS),
∴EG=FH;
(2) EG=FH,
EG=FH,
理由是:过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是菱形,
∴DC=AB=BC,AD∥BC,DC∥AB,
∵菱形ABCD的面积S=AB×GM=BC×HN,
∴GM=HN,
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
在△GME和△HNF中
∴△GME≌△HNF(AAS),
∴EG=FH.
(3)
=
,
理由是:过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,DC∥AB,
∵平行四边形ABCD的面积S=AB×GM=BC×HN,
∵AB=a,AD=b,
∴
=
,
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∴△GME∽△HNF,
∴
=
=
,
故答案为:
=
.
理由是:
 过G作GM⊥AB于M,过H作HN⊥BC于N,
过G作GM⊥AB于M,过H作HN⊥BC于N,∵四边形ABCD是正方形,
∴DC=AB,AD∥BC,DC∥AB,AD=BC,∠D=∠A=∠B=∠C=90°,
∴GM∥AD∥BC,HN∥DC∥AB,
∴四边形ADGM、四边形GMBC、四边形AHNB,四边形DCNH是平行四边形,
∴DC=HN=AB,AD=GM=BC,
∴HN=GM,
∵∠ADC=∠HOE=90°,
∴∠DHO+∠DGE=360°-90°-90°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∵HN⊥BC,GM⊥AB,
∴∠GME=∠HNF=90°,
在△GME和△HNF中
|
∴△GME≌△HNF(AAS),
∴EG=FH;
(2)
 EG=FH,
EG=FH,理由是:过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是菱形,
∴DC=AB=BC,AD∥BC,DC∥AB,
∵菱形ABCD的面积S=AB×GM=BC×HN,
∴GM=HN,
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
在△GME和△HNF中
|
∴△GME≌△HNF(AAS),
∴EG=FH.
(3)
| EG |
| FH |
| b |
| a |

理由是:过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,DC∥AB,
∵平行四边形ABCD的面积S=AB×GM=BC×HN,
∵AB=a,AD=b,
∴
| GM |
| HN |
| b |
| a |
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∴△GME∽△HNF,
∴
| EG |
| FH |
| GM |
| HN |
| b |
| a |
故答案为:
| EG |
| FH |
| b |
| a |
点评:本题考查了正方形性质,平行四边形性质,菱形性质,面积公式,全等三角形的性质和判定,相似三角形的性质和判定的应用,题目具有一定的代表性,证明过程类似.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 (2012•南湖区二模)用如图两个完全相同的直角三角板,下列图形中不能拼成的是( )
(2012•南湖区二模)用如图两个完全相同的直角三角板,下列图形中不能拼成的是( )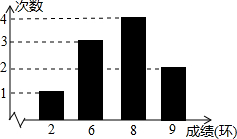 (2012•南湖区二模)如图是某选手10次射击成绩条形统计图,根据图中信息,下列说法错误的是( )
(2012•南湖区二模)如图是某选手10次射击成绩条形统计图,根据图中信息,下列说法错误的是( )