题目内容
已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .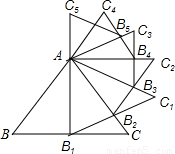
【答案】分析:由AB1为边长为2等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出第一个等边三角形AB1C1的面积,同理求出第二个等边三角形AB2C2的面积,依此类推,得到第n个等边三角形ABnCn的面积.
解答:解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=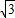 ,
,
∴第一个等边三角形AB1C1的面积为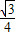 ×(
×( )2=
)2= (
( )1;
)1;
∵等边三角形AB1C1的边长为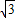 ,AB2⊥B1C1,
,AB2⊥B1C1,
∴B1B2=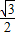 ,AB1=
,AB1= ,
,
根据勾股定理得:AB2= ,
,
∴第二个等边三角形AB2C2的面积为 ×(
×( )2=
)2=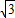 (
( )2;
)2;
依此类推,第n个等边三角形ABnCn的面积为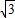 (
( )n.
)n.
故答案为: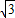 (
( )n
)n
点评:此题考查了等边三角形的性质,属于规律型试题,熟练掌握等边三角形的性质是解本题的关键.
解答:解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=
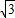 ,
,∴第一个等边三角形AB1C1的面积为
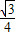 ×(
×( )2=
)2= (
( )1;
)1;∵等边三角形AB1C1的边长为
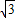 ,AB2⊥B1C1,
,AB2⊥B1C1,∴B1B2=
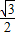 ,AB1=
,AB1= ,
,根据勾股定理得:AB2=
 ,
,∴第二个等边三角形AB2C2的面积为
 ×(
×( )2=
)2=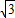 (
( )2;
)2;依此类推,第n个等边三角形ABnCn的面积为
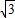 (
( )n.
)n.故答案为:
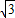 (
( )n
)n点评:此题考查了等边三角形的性质,属于规律型试题,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目


 14、如图所示,已知等边三角形ABC的边长为 1,按图中所示的规律,用2011个这样的等边三角形镶嵌而成的四边形的周长是
14、如图所示,已知等边三角形ABC的边长为 1,按图中所示的规律,用2011个这样的等边三角形镶嵌而成的四边形的周长是
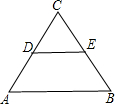 如图,已知等边三角形ABC的边长为2,DE是它的中位线,
如图,已知等边三角形ABC的边长为2,DE是它的中位线,