题目内容
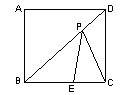
按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的面积为 

50
延长BG,交AE与点C,则易证△ABC是等腰直角三角形,因而AB=A,则CE=5,△CED是等腰直角三角形,则CD=5 ,根据CD=GF,即中间的小正方形的边长是5
,根据CD=GF,即中间的小正方形的边长是5 ,因而面积是50 .
,因而面积是50 .

解:延长BG,交AE与点C,
∵∠ABC=45°
∴△ABC是等腰直角三角形,
∴AB=AC
∴CE=5
∵△CED是等腰直角三角形,
∴CD=5
∵CD=GF,
∴中间的小正方形的边长是5 ,因而面积是50.
,因而面积是50.
故答案为50
能够注意到延长BG交AE与C,从而把问题转化为求直角三角形的边的问题,是解决本题的基本思路.
 ,根据CD=GF,即中间的小正方形的边长是5
,根据CD=GF,即中间的小正方形的边长是5 ,因而面积是50 .
,因而面积是50 .
解:延长BG,交AE与点C,
∵∠ABC=45°
∴△ABC是等腰直角三角形,
∴AB=AC
∴CE=5
∵△CED是等腰直角三角形,
∴CD=5

∵CD=GF,
∴中间的小正方形的边长是5
 ,因而面积是50.
,因而面积是50.故答案为50
能够注意到延长BG交AE与C,从而把问题转化为求直角三角形的边的问题,是解决本题的基本思路.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目


 进行绿化和硬化.设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形
进行绿化和硬化.设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形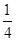 ,求P、Q两块绿地周围的硬化路面的宽
,求P、Q两块绿地周围的硬化路面的宽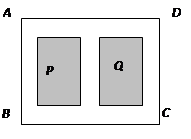

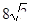 B.
B. 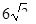 C.
C. 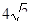 D.
D. 
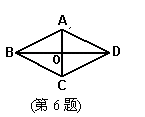
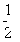 S四边形ABCD
S四边形ABCD