题目内容
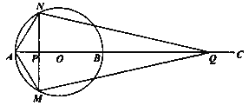
【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t=时,四边形AMQN为菱形;当t=时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
【答案】(1)![]() ,
,![]() ;(2)AC=3,t=1.
;(2)AC=3,t=1.
【解析】
(1)AP=t,CQ=t,则PQ=5-2t,由于NM⊥AB,根据垂径定理得PM=PN,根据菱形的判定方法,当PA=PQ时,四边形AMQN为菱形,即t=5-2t,然后解一元一次方程可求t的值;根据切线的判定定理,当∠ONQ=90时,NQ与⊙O相切,如图,此时OP=t-1,OQ=AC-OA-QC=4-t,再证明Rt△ONP∽Rt△ONQ,利用相似比可得t2-5t+5=0,然后解一元二次方程可得到t的值;
(2)当四边形AMQN为正方形,则∠MAN=90,又可判断AQ为直径,于是得到点P在圆心,所以t=AP=1,CQ=t=1,则得到此时AC=AQ+CQ=3.
(1)![]() ,
,![]() ;
;
(2)当AC的长为3时,存在t=1,使四边形AMQN为正方形.理由如下:
∵四边形AMQN为正方形.
∴∠MAN=90.∴MN为⊙O的直径;
∴MN=AQ=2.∴t=AP=![]() =1,
=1,
又∵CQ=t=1,∴AC=AQ+CQ=2+1=3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目