题目内容
【题目】如图，在平面直角坐标系中，点A的坐标为(4，0)，点P是第一象限内直线y＝－x＋6上一点．O是坐标原点．
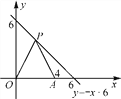
(1)设P(x，y)，求△OPA的面积S与x的函数解析式；
(2)当S＝10时，求P点的坐标；
(3)在直线y＝－x＋6上求一点P，使△POA是以OA为底边的等腰三角形．
【答案】(1) S＝－2x＋12(0＜x＜6)(2) P点的坐标为(1，5)(3)P(2，4)
【解析】（1）由于点P在直线x+y=6上，得点P的纵坐标为6-x，根据三角形面积公式即可求解；
（2）当S=10时，代入即可求解；
（3）由题意分析可知，OA的垂直平分线与x+y=6的交点即为所求的P点，所以即可求出点P．
解：(1)∵点P在直线y＝－x＋6上，
∴点P的纵坐标为6－x.
∴S＝
×4×(6－x)＝－2x＋12(0＜x＜6)．
(2)当S＝10时，则－2x＋12＝10，
∴x＝1.
∴y＝－1＋6＝5.
∴P点的坐标为(1，5)．
(3)由题意分析可知，OA的垂直平分线与y＝－x＋6的交点即为所求的点P，
∴P点的横坐标为2，
∴y＝4.
∴P(2，4)．
练习册系列答案
相关题目
