Question

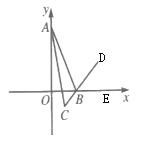
【题目】如图，在平面直角坐标系中，点，分别在轴，轴正半轴上．

（1）的平分线与的外角平分线交于点，求的度数；

（2）设点，的坐标分别为，，且满足，求的面积；

（3）在（2）的条件下，当是以为斜边的等腰直角三角形时，请直接写出点的坐标．

Answer 1

【答案】（1）45°；（2）1；（3）（1.5，1.5）或（-0.5，0.5）

【解析】

（1）根据角平分线的定义即可得出∠BAC=∠OAB、∠DBA=∠EBA，再根据三角形的外角的性质即可得出∠C=∠AOB=45°；
（2）利用非负数的性质求出a，b的值，即可求得的面积；

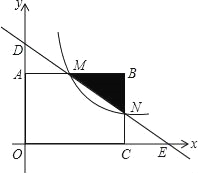
（3）作DE⊥x轴于E，DF⊥y轴与F，可得△DEB≌△DFA，则BE=AF，DF=DE，推出四边形OEDF是正方形，OE=OF，设BE=AF=x，则OA-x=OB+x,求出x的值，即可得的坐标，同理求出点D1的坐标．

解：（1）∵AC平分∠OAB，BD平分∠EBA，
∴∠BAC=∠OAB、∠DBA=∠EBA，
∵∠EBA=∠OAB+∠AOB，
∴∠DBA=（∠OAB+∠AOB）=∠C+∠CAB，
∴∠C=（∠OAB+∠AOB）-∠CAB

=（∠OAB+∠AOB）-∠OAB

=∠AOB

=45°；

（2）∵且满足，

∴

∴a=2，b=1，

∵点，的坐标分别为，，

∴OA=2，OB=1，

∴=；

（3）作DE⊥x轴于E，DF⊥y轴与F，

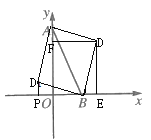
∵是以为斜边的等腰直角三角形，

∴AD=BD，∠ADB=90°，

∵DE⊥x轴于E，DF⊥y轴与F，∠AOB=90°，

∴四边形OEDF是矩形，∠BED=∠AFD=90°，

∴∠EDF=90°，

∴∠EDB=∠FDA，

∴△DEB≌△DFA，

∴BE=AF，DF=DE，

∴四边形OEDF是正方形，

∴OE=OF，

设BE=AF=x，则OA-x=OB+x,

∵OA=2，OB=1，

∴x=0.5，OE=OF=1.5，

∴的坐标为（1.5，1.5），

同理可得PD1=0.5，OP=1.5-1=0.5，

D1的坐标为（-0.5，0.5），

即的坐标为（1.5，1.5）或（-0.5，0.5）．