Question

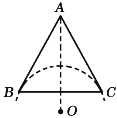
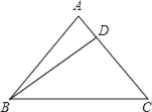
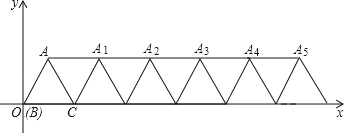
【题目】如图，在平面直角坐标系内，边长为4的等边△ABC的顶点B与原点重合，将△ABC绕顶点C顺时针旋转60°得到△ACA1，将四边形ABCA1看作一个基本图形，将此基本图形不断复制并平移，请回答：

(1)点A的坐标为　 　；点A1的坐标为　 　．

(2)A2018的坐标为　 　．

Answer 1

【答案】(1)（2，2）；（6，2）；(2)（8074，2）.

【解析】

(1) 边长为4的等边△ABC的顶点B与原点重合,可得OA＝BC＝4，∠AOC＝60°，过点A作AD⊥x轴于点D，求出A点坐标，再根据ABCA1是平行四边形得出A1的坐标；

(2)将四边形ABCA1看作一个基本图形，将此基本图形不断复制并平移，最后得出A2018的坐标.

(1)∵边长为4的等边△ABC的顶点B与原点重合，

∴OA＝BC＝4，∠AOC＝60°．

如图，过点A作AD⊥x轴于点D，

∴BD＝DC＝BC＝2，AD＝2，

∴点A的坐标为（2，2）．

∵将△ABC绕顶点C顺时针旋转60°得到△ACA1，

∴四边形ABCA1是平行四边形，

∴AA1＝BC＝4，AA1∥BC，

∴点A1的坐标为（2+4，2），即（6，2）．

故答案为：（2，2）；（6，2）．

(2)∵将四边形ABCA1看作一个基本图形，将此基本图形不断复制并平移，

∴点A2的坐标为（2+4×2，2），即（10，2）；点A3的坐标为（2+4×3，2），即（14，2）；……；

∴点A2018的坐标为（2+4×2018，2），即（8074，2）．

故答案为：（8074，2）．