题目内容
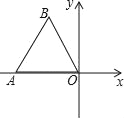
【题目】如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为_____.
【答案】(﹣![]() ,﹣
,﹣![]() )
)
【解析】
作BC⊥x轴于C,如图,根据等边三角形的性质得OA=OB=1,AC=OC=![]() ,
,
∠BOA=60°,则易得A点坐标和O点坐标,再利用勾股定理计算出BC=![]() ,然后根据第二象限点的坐标特征可写出B点坐标;由旋转的性质得∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,则点A′与点B关于x轴对称,于是可得点A′的坐标.
,然后根据第二象限点的坐标特征可写出B点坐标;由旋转的性质得∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,则点A′与点B关于x轴对称,于是可得点A′的坐标.
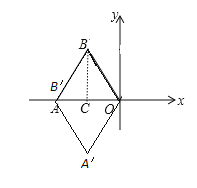
作BC⊥x轴于C,如图,∵△ABO是边长为1的等边三角形,
∴OA=OB=1,AC=OC=![]() ,∠BOA=60°,
,∠BOA=60°,
∴A点坐标为(-1, 0),O点坐标为(0, 0),
在Rt△BOC中,BC=![]() ,
,
∴B点坐标为(![]() ,
,![]() );
);
∵将△ABO按逆时针方向旋转60°,得到△OA′B′,
∴∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,
∴点B′与点A重合,点A′与点B关于x轴对称,即点A′的坐标为(![]() ,
,![]() ).
).
故答案为:![]() ,
,![]() ).
).

练习册系列答案
相关题目