题目内容
(2011•虹口区一模)如图,在矩形ABCD中,AB=4,AD=2,点M是AD的中点.点E是边AB上的一动点,连接EM并延长交射线CD于点F,过M作EF的垂线交BC的延长线于点G,连接EG,交边DC于点Q.设AE的长为x,△EMG的面积为y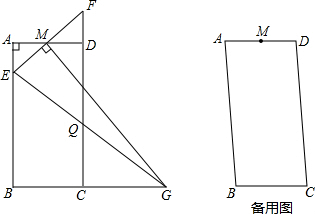
(1)求∠MEG的正弦值;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)线段MG的中点记为点P,连接CP,若△PGC∽△EFQ,求y的值.

(1)求∠MEG的正弦值;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)线段MG的中点记为点P,连接CP,若△PGC∽△EFQ,求y的值.
分析:(1)先过点G作GN⊥AD交AD的延长线于点N,可证得△AEM∽△NMG,得出GN的值,再根据M是AD的中点,得出AM=1,即可得出
=
的比值,从而得出∠MEG的正切值,根据勾股定理求出EG,即可求出∠MEG的正弦值;
(2)由(1)知,MG=4EM,在Rt△AEM中,得出MG=4
,根据S△EMG=
EM•MG,即可求出函数解析式,并得出x的取值范围;
(3)先分别过点P、M作PH、MI垂直BG于点H,I,得出BE、IG、BG、CF、CG、CH的值,即可得出EF=PG,∠F=∠PGC,再根据△PGC∽△EFQ,得出∠QEF=∠CPG即可得出y的值.
| MG |
| EM |
| GN |
| MA |
(2)由(1)知,MG=4EM,在Rt△AEM中,得出MG=4
| x2+1 |
| 1 |
| 2 |
(3)先分别过点P、M作PH、MI垂直BG于点H,I,得出BE、IG、BG、CF、CG、CH的值,即可得出EF=PG,∠F=∠PGC,再根据△PGC∽△EFQ,得出∠QEF=∠CPG即可得出y的值.
解答: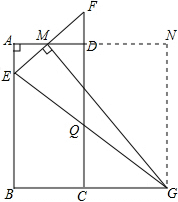 解:(1)过点G作GN⊥AD交AD的延长线于点N,可证得△AEM∽△NMG,
解:(1)过点G作GN⊥AD交AD的延长线于点N,可证得△AEM∽△NMG,
∴
=
,
∴GN=AB=4,
∵M是AD的中点,
∴AM=1,
∴
=
=4,
∵GM⊥EF,
∴在Rt△EMG中,
∴tan∠MEG=
=4;
设MG=4x,EM=x,在△EMG中,由勾股定理得:EG=
=
x,
∴sin∠MEG=
=
=
,
即∠MEG的正弦值是
;
(2)由(1)知,
=4,即MG=4EM,
∵在Rt△AEM中,EM=
,
∴MG=4
,
∵S△EMG=
EM•MG,
∴y=2x2+2 (
<x≤4);
(3)分别过点P、M作PH、MI垂直BG于点H,I,
∴BE=4-x,IG=4x,
∴BG=4x+1,CF=x+4,CG=4x-1,CH=2x-1,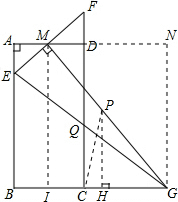
∴EF=PG,∠F=∠PGC,
∵△PGC∽△EFQ,
∴∠QEF=∠CPG,
则可证:△CPG≌△QEF,
∴QF=CG=4x-1,
∴CQ=CF-QF=5-3x,
可证BE∥CQ,
∴
=
,即CG•BE=CQ•BG,
∴(4x-1)(4-x)=(5-3x)(4x+1),
解得:x1=
,x2=-
(舍去),
∴y=
;
∴可知y的值是
.
 解:(1)过点G作GN⊥AD交AD的延长线于点N,可证得△AEM∽△NMG,
解:(1)过点G作GN⊥AD交AD的延长线于点N,可证得△AEM∽△NMG,∴
| MG |
| EM |
| GN |
| MA |
∴GN=AB=4,
∵M是AD的中点,
∴AM=1,
∴
| MG |
| EM |
| GN |
| MA |
∵GM⊥EF,
∴在Rt△EMG中,
∴tan∠MEG=
| MG |
| EM |
设MG=4x,EM=x,在△EMG中,由勾股定理得:EG=
| (4x)2+x2 |
| 17 |
∴sin∠MEG=
| MG |
| EG |
| 4x | ||
|
4
| ||
| 17 |
即∠MEG的正弦值是
4
| ||
| 17 |
(2)由(1)知,
| MG |
| EM |
∵在Rt△AEM中,EM=
| x2+1 |
∴MG=4
| x2+1 |
∵S△EMG=
| 1 |
| 2 |
∴y=2x2+2 (
| 1 |
| 4 |
(3)分别过点P、M作PH、MI垂直BG于点H,I,
∴BE=4-x,IG=4x,
∴BG=4x+1,CF=x+4,CG=4x-1,CH=2x-1,

∴EF=PG,∠F=∠PGC,
∵△PGC∽△EFQ,
∴∠QEF=∠CPG,
则可证:△CPG≌△QEF,
∴QF=CG=4x-1,
∴CQ=CF-QF=5-3x,
可证BE∥CQ,
∴
| CG |
| BG |
| CQ |
| BE |
∴(4x-1)(4-x)=(5-3x)(4x+1),
解得:x1=
| 3 |
| 4 |
| 2 |
| 3 |
| 4 |
| 2 |
∴y=
| 17 |
| 4 |
∴可知y的值是
| 17 |
| 4 |
点评:此题考查了相似三角形的判定与性质;解题的关键是根据矩形的性质,锐角三角函数的定义分别进行解答.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
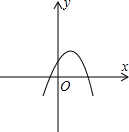 (2011•虹口区一模)已知抛物线y=ax2+bx+c(a≠0)如图所示,下列结论中,正确的是( )
(2011•虹口区一模)已知抛物线y=ax2+bx+c(a≠0)如图所示,下列结论中,正确的是( ) (2011•虹口区一模)如图,在Rt△ABC中,DE∥BC,AD=
(2011•虹口区一模)如图,在Rt△ABC中,DE∥BC,AD=