题目内容
【题目】如图①,在四边形ABCD中,AD∥BC,∠C=90°,CD=6cm.动点Q从点B出发,以1cm/S的速度沿BC运动到点C停止,同时,动点P也从B点出发,沿折线B→A→D运动到点D停止,且PQ⊥BC.设运动时间为t(s),点P运动的路程为y(cm),在直角坐标系中画出y关于t的函数图象为折线段OE和EF(如图②).已知点M(4,5)在线段OE上,则图①中AB的长是________cm.
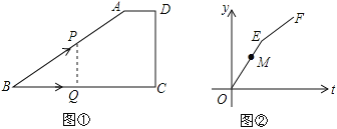
【答案】10
【解析】
先根据点M求得OE的解析式,再利用矩形ADCG的性质得到AG的长,最后在Rt△ABG中,利用勾股定理得到t的值,从而得到AB.
设OE的解析式为y=kt,
∵点M(4,5),
∴k= ![]() ,
,
如下图
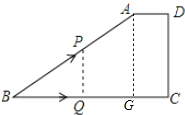
当Q运动到G点时,点P运动到A点,BQ=t,AB= ![]() ,
,
∵AG⊥BC,
∴四边形ADCG是矩形,
∴AG=DC=6,
∴AB2=BG2+AG2 ,
∴( ![]() )2=t2+62 ,
)2=t2+62 ,
解得:t=8,
∴AB= ![]() ×8=10(cm).
×8=10(cm).

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目