题目内容
如图,△ABC中,∠BAC=90°,AC=2,AB=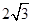 ,△ACD是等边三角形.
,△ACD是等边三角形.
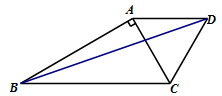
(1)求∠ABC的度数.
(2)以点A为中心,把△ABD顺时针旋转60°,画出旋转后的图形.
(3)求BD的长度.
 ,△ACD是等边三角形.
,△ACD是等边三角形.
(1)求∠ABC的度数.
(2)以点A为中心,把△ABD顺时针旋转60°,画出旋转后的图形.
(3)求BD的长度.
解:(1)根据勾股定理求得BC=4,在 Rt△ABC中AC=2∴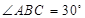 °;
°;
(2)如图
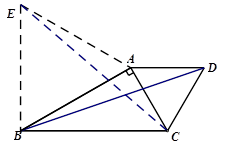
(3)连接BE.
由(2)知:△ACE≌△ADB
∴AE=AB,∠BAE=60°,BD=EC
∴BE= AE=AB=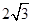 ,∠EBA=60°
,∠EBA=60°
∴∠EBC=90°
又BC=2AC=4
∴Rt△EBC中,EC=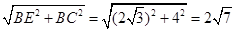
∴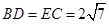
方法2:过点D作DF⊥BC,交BC延长线于点F,
则求得EF=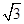
BF =5,
∴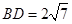
方法3:过点D作DG⊥BA,交BA延长线于点G,按照方法2给分。
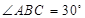 °;
°;(2)如图

(3)连接BE.
由(2)知:△ACE≌△ADB
∴AE=AB,∠BAE=60°,BD=EC
∴BE= AE=AB=
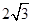 ,∠EBA=60°
,∠EBA=60°∴∠EBC=90°
又BC=2AC=4
∴Rt△EBC中,EC=
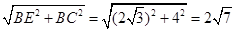
∴
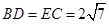
方法2:过点D作DF⊥BC,交BC延长线于点F,
则求得EF=
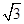
BF =5,
∴
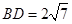
方法3:过点D作DG⊥BA,交BA延长线于点G,按照方法2给分。
(1)利用正切的知识可得出答案.
(2)根据旋转角度、旋转中心、旋转方向找出各点的对称点,顺次连接即可;
(3)根据旋转的性质可得△ACE≌△ADB,从而确定∠EBC=90°,然后利用勾股定理即可解答.
(2)根据旋转角度、旋转中心、旋转方向找出各点的对称点,顺次连接即可;
(3)根据旋转的性质可得△ACE≌△ADB,从而确定∠EBC=90°,然后利用勾股定理即可解答.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

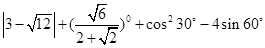 ;
;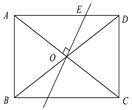
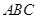 中,∠
中,∠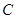 =90°,那么下列各式中,正确的是( )
=90°,那么下列各式中,正确的是( )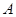 .
.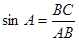 ;
; 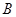 .
.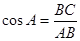 ;
; 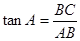 ;
; 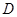 .
.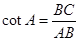 .
.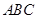 中,
中,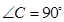 ,
,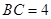 ,
,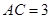 ,将△
,将△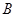 旋转后点
旋转后点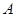 落在直线
落在直线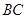 上的点
上的点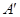 ,点
,点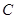 落在点
落在点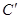 处,那么
处,那么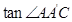 的值是 .
的值是 .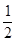 ,则∠A= ;若a=5,c=13,则tanA=
,则∠A= ;若a=5,c=13,则tanA=