题目内容
【题目】如图,AE、BD是![]() 的高,AE,BD交于点C,且AE=BE,BD平分
的高,AE,BD交于点C,且AE=BE,BD平分![]() .
.

(1)求证:BC=2AD
(2)求![]() 的度数.
的度数.
【答案】(1)详见解析;(2)45°.
【解析】
(1)证△ABD≌△MBD,推出AD=DM=![]() AM,由△AME≌△BCE,推出AM=BC,即可得出答案.
AM,由△AME≌△BCE,推出AM=BC,即可得出答案.
(2)根据等腰三角形两底角相等列式计算即可得解.
(1)∵BD平分∠ABM,BD是高,
∴∠ABD=∠MBD,∠ADB=∠MDB=90°,
∵在△ABD和△MBD中,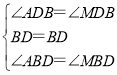 ,
,
∴△ABD≌△MBD(ASA),
∴AD=DM=![]() AM,
AM,
∵△AME≌△BCE,
∴AM=BC,
∴BC=2AD.
(2)∵AE是△ABM的高,AE=BE,
∴△ABE是等腰直角三角形,
∴∠EAB=∠EBA=45°,
∵BD平分∠ABM,
∴∠ABD=∠MBD=22.5°,
∵BD是△ABM的高,
∴∠MAE=∠MBD=22.5°,
∴∠MAB=∠M=∠BCE=67.5°,
∵AD=MD,
∴DE=AD=MD,
∴∠MDE=180°-2×67.5°=45°.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目