题目内容
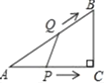
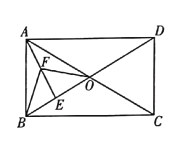
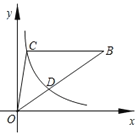
【题目】如图,△OBC的边BC∥x轴,过点C的双曲线y=![]() (k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
【答案】2
【解析】
延长BC交y轴于点E,过点D作DF⊥x轴于点FBA⊥x轴于A.由矩形与反比例函数的性质,可得S四边形ABDF=S△OBC=8,易证得△ODF∽△OBA,又由OD:DB=1:2,即可得S△ODF=![]() S四边形ABDF=
S四边形ABDF=![]() ×4=
×4=![]() ,则可求得答案.
,则可求得答案.
解:延长BC交y轴于点E,过点D作DF⊥x轴于点F,BA⊥x轴于A.
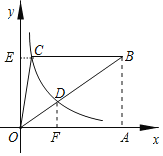
∵梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,
∴四边形OABE是矩形,
∴S△OBE=S△OAB,
∵过点C的双曲线y=![]() 交OB于点D,
交OB于点D,
∴S△OCE=S△ODF,
∴S四边形ABDF=S△OBC=8,
∵DF∥AB,
∴△ODF∽△OBA,
∵OD:DB=1:2,
∴OD:OB=1:3,
∴S△ODF:S△OAB=1:9,
∴S△ODF:S四边形ABDF=1:8,
∴S△ODF=![]() S四边形ABDF=
S四边形ABDF=![]() ×8=1,
×8=1,
∴k=2.
故答案为:2.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
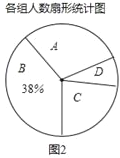
新黄冈兵法密卷系列答案【题目】为庆祝建国70周年,某校举办了爱我中华知识竞赛活动.该校南、北两个校区七年级各有300名学生参加竞赛活动.为了解这两个校区参赛学生成绩情况,从中各随机抽取了10名学生的成绩进行调查,过程如下:
(收集、整理、描述数据)根据随机抽取的10名学生的成绩,制作了如下统计图表:
(说明:成绩90分及以上为优秀,80-89分为良好,60-79分为合格,60分以下为不合格)
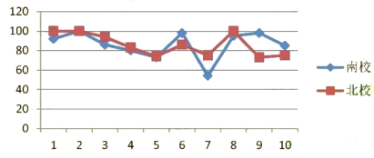
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
(分析数据)对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数如下表:
校区 | 平均数(分) | 中位数(分) | 众数(分) |
南校 | 87 | 90.5 | |
北校 | 86 | 100 |
(得出结论)综合上述统计全过程,回答下列问题:
(1)补全表格.
(2)估计北校七年级学生竞赛成绩为优秀的人数.
(3)你认为哪个校区的七年级学生竞赛成绩比较好?说明你的理由.(从两个不同的角度说明推断的合理性)
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全区范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽部分使用电瓶车的市民,就骑电瓶车戴安全帽情况(![]() :每次戴、
:每次戴、![]() :经常戴、
:经常戴、![]() :偶尔戴、
:偶尔戴、![]() :都不戴)进行问卷调查,将相关的数据制成如下统计图表.
:都不戴)进行问卷调查,将相关的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
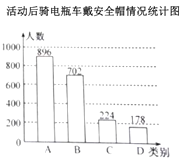
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该区约有37万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,谈谈你对交警部门宣传活动的效果的看法.