题目内容
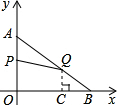
如图,在平面直角坐标系中,已知点A(0,6),B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P,Q移动的时间为t(s).当t为何值时,△APQ与△AOB相似?并求出此时点P与点Q的坐标.


若△APQ与△AOB相似,有两种情况.
∵OA=6,OB=8,∠AOB=90°,
∴AB=10.设Q点的坐标是(x,y).
(1)当P与O对应时,△APQ∽△AOB,
=
,
=
,即t=
s,
∴AP=
,
∴OP=0A-AP=
.
∴BQ=
,
∴x=OB-BQ•cosB=8-
×
=
,
过Q作QC⊥OB于C,
y=QC=QBsinB=
,
P(0,
),Q(
,
)
(2)当P与O对应时,△APQ∽△AOB,
∴
=
,即
=
,
解得:t=
,
∴AP=
,OP=OA-AP=
,
∴BQ=
,
∴x=OB-BQ•cosB=8-
×
=
,y=QBsinB=
×
=
.
所以P(0,
),Q(
,
),
当P与B对应时,△APQ∽△ABO,
∴
=
,即
=
,
解得:t=
,
∴AP=
,OP=OA-AP=
.
∴BQ=
,
∴x=OB-BQ•cosB=8-
×
=
,y=QBsinB=
×
=
.
所以P(0,
)Q(
,
),
综上,P(0,
),Q(
,
)或者P(0,
)Q(
,
).
∵OA=6,OB=8,∠AOB=90°,
∴AB=10.设Q点的坐标是(x,y).
(1)当P与O对应时,△APQ∽△AOB,
| AP |
| AO |
| AQ |
| AB |
| t |
| 6 |
| 10-2t |
| 10 |
| 30 |
| 11 |
∴AP=
| 30 |
| 11 |
∴OP=0A-AP=
| 36 |
| 11 |
∴BQ=
| 60 |
| 11 |
∴x=OB-BQ•cosB=8-
| 60 |
| 11 |
| 8 |
| 10 |
| 40 |
| 11 |
过Q作QC⊥OB于C,
y=QC=QBsinB=
| 36 |
| 11 |
P(0,
| 36 |
| 11 |
| 40 |
| 11 |
| 36 |
| 11 |
(2)当P与O对应时,△APQ∽△AOB,
∴
| AP |
| AO |
| AQ |
| AB |
| t |
| 6 |
| 10-2t |
| 10 |
解得:t=
| 30 |
| 11 |
∴AP=
| 30 |
| 11 |
| 36 |
| 11 |
∴BQ=
| 60 |
| 11 |
∴x=OB-BQ•cosB=8-
| 60 |
| 11 |
| 8 |
| 10 |
| 40 |
| 11 |
| 60 |
| 11 |
| 6 |
| 10 |
| 36 |
| 11 |
所以P(0,
| 36 |
| 11 |
| 40 |
| 11 |
| 36 |
| 11 |
当P与B对应时,△APQ∽△ABO,
∴
| AP |
| AB |
| AQ |
| AO |
| t |
| 10 |
| 10-2t |
| 6 |
解得:t=
| 50 |
| 13 |
∴AP=
| 50 |
| 13 |
| 28 |
| 13 |
∴BQ=
| 100 |
| 13 |
∴x=OB-BQ•cosB=8-
| 100 |
| 13 |
| 8 |
| 10 |
| 24 |
| 13 |
| 100 |
| 13 |
| 6 |
| 10 |
| 60 |
| 13 |
所以P(0,
| 28 |
| 13 |
| 24 |
| 13 |
| 60 |
| 13 |
综上,P(0,
| 36 |
| 11 |
| 40 |
| 11 |
| 36 |
| 11 |
| 28 |
| 13 |
| 24 |
| 13 |
| 60 |
| 13 |


练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目