Question

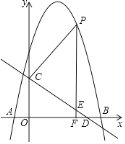
【题目】如图，在平面直角坐标系xOy中，抛物线与x轴相交于点A（﹣2，0）、B（4，0），与y轴交于点C（0，﹣4），BC与抛物线的对称轴相交于点D．

（1）求该抛物线的表达式，并直接写出点D的坐标；

（2）过点A作AE⊥AC交抛物线于点E，求点E的坐标．

Answer 1

【答案】（1）y=x2﹣x﹣4，D（1，﹣3）；（2）E（5，）

【解析】

（1）设抛物线的解析式为y=a(x+2)(x4), 将C(0,4)代入求解即可；记抛物线的对称轴与x轴交点坐标为F．先求得抛物线的对称轴，则可得到FB的长，然后再证明△BFD为等腰直角三角形，从而可得到FD=FB=3，故此可得到点D的坐标；
（2）过点E作EH⊥AB，垂足为H．先证∠EAH=∠ACO，则tan∠EAH=tan∠ACO=.设EH=t，则AH=2t，从而可得到E（-2+2t，t），最后，将点E的坐标代入抛物线的解析式求解即可；

(1)设抛物线的解析式为y=a(x+2)(x4),将C(0,4)代入得：8a=4,解得：

∴抛物线的解析式为

如下图所示：记抛物线的对称轴与x轴交点坐标为F.

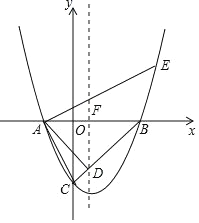
∵抛物线的对称轴为

∴BF=OBOF=3.

∵BO=OC=4,

∴

∴△BFD为等腰直角三角形,

∴FD=FB=3.

∴D(1,3).

(2)如下图，过点E作EH⊥AB，垂足为H.

∵

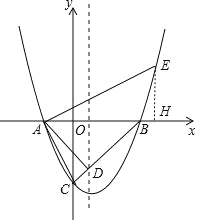
∴∠EAH=∠ACO.

∴tan∠EAH=tan∠ACO=.

设EH=t，则AH=2t，

∴点E的坐标为(2+2t,t).

将(2+2t,t)代入抛物线的解析式得：

解得：或t=0(舍去)

∴