题目内容
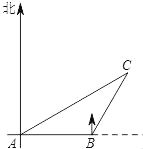
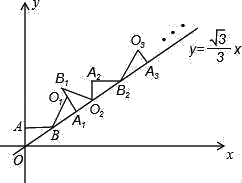
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=![]() x上,依次进行下去…,若点A的坐标是(0,1),则点A8的横坐标是_____
x上,依次进行下去…,若点A的坐标是(0,1),则点A8的横坐标是_____
【答案】6![]() +6
+6
【解析】
由题知,△AOB为直角三角形,且求出OA=1,AB=![]() ,OB=2;观察可知,△AOB的边都落在直线
,OB=2;观察可知,△AOB的边都落在直线![]() 上,而直线与x轴夹角为30°,则可求出A1的横坐标为(OB+AB)×cos30°;A2的横坐标为(OB+AB+AO)×cos30°,以此类推,找出其中的规律,即可求得A8的横坐标.
上,而直线与x轴夹角为30°,则可求出A1的横坐标为(OB+AB)×cos30°;A2的横坐标为(OB+AB+AO)×cos30°,以此类推,找出其中的规律,即可求得A8的横坐标.
∵点A和点B的纵坐标都为1,
∴AB∥x轴,即AB⊥y轴,
∴△AOB为直角三角形,
OA=1,AB=![]() ,由勾股定理得
,由勾股定理得
![]()
∴OA1=OB+BA1=OB+AB=2+![]() ,
,
由B(![]() ,1)可知,直线
,1)可知,直线![]() 与x轴夹角的正切值为
与x轴夹角的正切值为![]()
则直线![]() 与x轴夹角为30°,
与x轴夹角为30°,
则点A1横坐标的值为OA1×cos30°![]()
点A1纵坐标的值为OA1×sin30°=![]()
∴A1的坐标表示为![]()
以此类推,A2的坐标表示为![]() ,
,
A3的坐标表示为![]()
A4的坐标表示为![]()
根据探索的规律可知,A8的横坐标为![]()
故答案为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目