题目内容
正方形ABCD和正方形EFGH的边长分别为2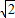 和
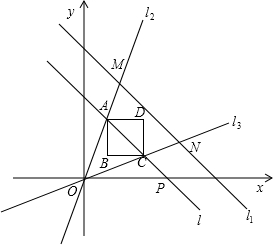
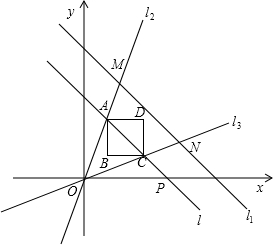
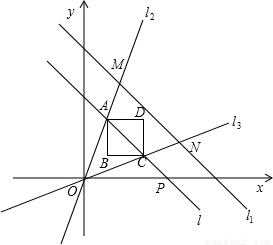
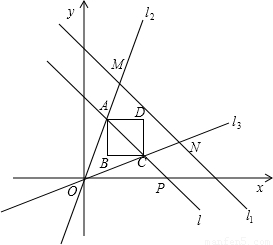
和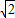 ,对角线BD和FH都在直线l上,O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距,当中心O2在直线l上平移时,正方形EFGH也随之平移(其形状大小没有变化).(所谓正方形的中心,是指正方形两条对角线的交点;两个正方形的公共点,是指两个正方形边的公共点)
,对角线BD和FH都在直线l上,O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距,当中心O2在直线l上平移时,正方形EFGH也随之平移(其形状大小没有变化).(所谓正方形的中心,是指正方形两条对角线的交点;两个正方形的公共点,是指两个正方形边的公共点)(1)当中心O2在直线l上平移到两个正方形只有一个公共点时,中心距O1O2=______;
(2)设计表格完成问题:随着中心O2在直线l上平移,两个正方形的公共点的个数的变化情况和相应的中心距的值或取值范围.
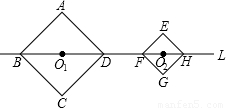
【答案】分析:(1)先根据正方形的性质求出正方形的对角线分别为BD=4,FH=2,所以可求得两个正方形只有一个公共点时,中心距O1O2=O1D+O2F=2+1=3;
(2)根据它们随着中心O2在直线l上平移,两个正方形的公共点的个数的变化情况和相应的中心距之间的关系可依次求解.
解答:解:根据题意可知:BD=4,FH=2;
(1)两个正方形只有一个公共点时,中心距O1O2=O1D+O2F=2+1=3;
(2)
点评:主要考查了正方形的性质和平移的性质.要掌握正方形中一些特殊的性质:四边相等,四角相等,对角线相等且互相垂直平分.
(2)根据它们随着中心O2在直线l上平移,两个正方形的公共点的个数的变化情况和相应的中心距之间的关系可依次求解.
解答:解:根据题意可知:BD=4,FH=2;
(1)两个正方形只有一个公共点时,中心距O1O2=O1D+O2F=2+1=3;
(2)
| O1O1 | 大于3 | 等于3 | 1<O1O2<3 | 等于1 | 0≤O1O2≤1 |
| 公共点的个数 | 1 | 2 | 无数个 |
点评:主要考查了正方形的性质和平移的性质.要掌握正方形中一些特殊的性质:四边相等,四角相等,对角线相等且互相垂直平分.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目