题目内容
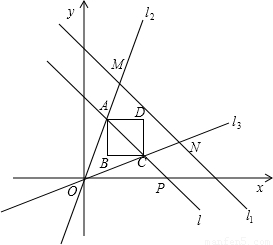
(2009•黄埔区一模)如图,直线l1:y=-x+1与两直线l2:y=2x,l3:y=x分别相交于M、N两点.设点P为x轴上的一点,过点P的直线l:y=-x+b与直线l2、l3分别交于A、C两点,以线段AC为对角线作正方形ABCD.(1)写出正方形ABCD各顶点的坐标(用b表示);
(2)当点P从原点O出发,沿着x轴的正方向运动时,设正方形ABCD和△OMN重叠部分的面积为S,求S与b之间的函数关系式,并写出自变量b的取值范围.
【答案】分析:(1)联立y=-x+b,y=2x求出点A,C的坐标.同理求出B,D的坐标.
(2)本题考查的是分段函数的有关知识.当D在l1上是b= ,B在l1上是b=
,B在l1上是b= ;然后根据实际分成
;然后根据实际分成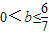 ;
;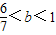 ;
;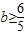 时三种情况,S的面积都不同.
时三种情况,S的面积都不同.
解答:解:(1)由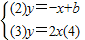 ,(5分)
,(5分)
得 ,(9分)
,(9分)
∴A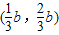 ,
,
同理C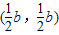 ,
,
∵四边形ABCD是正方形,
∴AB∥DC∥y轴,AD∥BC∥x轴,
可得B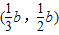 ,D
,D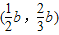 ;(4分)
;(4分)
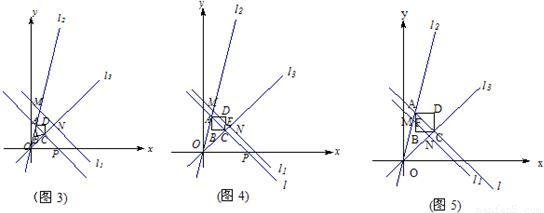
(2)当D在l1(11)上时(如图1),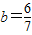 (12),
(12),
当B在l1(13)上时(如图2),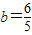 ;(6分)
;(6分)
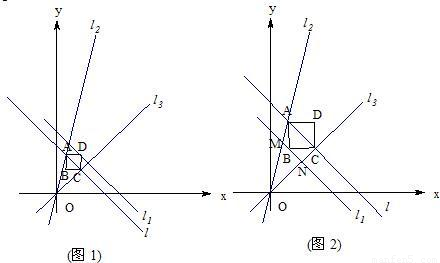
当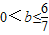 时(如图1、3),直线l在直线l1上或下方,点D在直线l1上或下方,
时(如图1、3),直线l在直线l1上或下方,点D在直线l1上或下方,
∵正方形ABCD的边长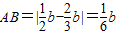 ,
,
∴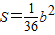 ;(8分)
;(8分)
当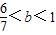 时(如图4),直线l在直线l1下方,点D在直线l1上方,
时(如图4),直线l在直线l1下方,点D在直线l1上方,
设DC与直线l1交于点E,则E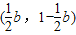
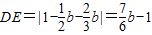 ,
,
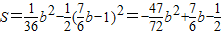 ;(10分)
;(10分)
当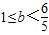 时,直线l在直线l1上或上方,且点B在l1下方,(如图5),若设AB与直线l1交于点F,则F
时,直线l在直线l1上或上方,且点B在l1下方,(如图5),若设AB与直线l1交于点F,则F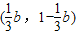 ,
, ,
,
∴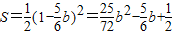 ;(12分)
;(12分)
当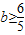 时,直线l在直线l1上方,且点B在l1上或上方(如图2),S=0.(14分)
时,直线l在直线l1上方,且点B在l1上或上方(如图2),S=0.(14分)
点评:本题考查的是一次函数的综合应用,重点是考查考生考虑问题的能力,要学会全面分析题目然后才得解.
(2)本题考查的是分段函数的有关知识.当D在l1上是b=
 ,B在l1上是b=
,B在l1上是b= ;然后根据实际分成
;然后根据实际分成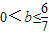 ;
;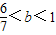 ;
;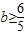 时三种情况,S的面积都不同.
时三种情况,S的面积都不同.解答:解:(1)由
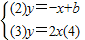 ,(5分)
,(5分)得
 ,(9分)
,(9分)∴A
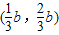 ,
,同理C
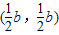 ,
,∵四边形ABCD是正方形,
∴AB∥DC∥y轴,AD∥BC∥x轴,
可得B
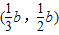 ,D
,D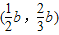 ;(4分)
;(4分)(2)当D在l1(11)上时(如图1),
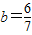 (12),
(12),当B在l1(13)上时(如图2),
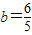 ;(6分)
;(6分)
当
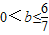 时(如图1、3),直线l在直线l1上或下方,点D在直线l1上或下方,
时(如图1、3),直线l在直线l1上或下方,点D在直线l1上或下方,∵正方形ABCD的边长
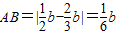 ,
,∴
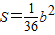 ;(8分)
;(8分)当
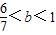 时(如图4),直线l在直线l1下方,点D在直线l1上方,
时(如图4),直线l在直线l1下方,点D在直线l1上方,设DC与直线l1交于点E,则E
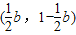
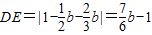 ,
,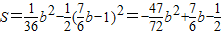 ;(10分)
;(10分)当
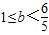 时,直线l在直线l1上或上方,且点B在l1下方,(如图5),若设AB与直线l1交于点F,则F
时,直线l在直线l1上或上方,且点B在l1下方,(如图5),若设AB与直线l1交于点F,则F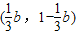 ,
, ,
,∴
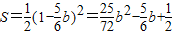 ;(12分)
;(12分)当
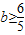 时,直线l在直线l1上方,且点B在l1上或上方(如图2),S=0.(14分)
时,直线l在直线l1上方,且点B在l1上或上方(如图2),S=0.(14分)
点评:本题考查的是一次函数的综合应用,重点是考查考生考虑问题的能力,要学会全面分析题目然后才得解.

练习册系列答案
相关题目
 .
.