题目内容
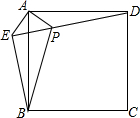 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=| 6 |
①△APD≌△AEB﹔②点B到直线AE的距离为
| 3 |
| 2 |
其中正确结论的序号是( )
分析:根据正方形的性质可得AB=AD,再根据同角的余角相等求出∠BAE=∠DAP,然后利用“边角边”证明△APD和△AEB全等,从而判定①正确,根据全等三角形对应角相等可得∠AEB=∠APD=135°,然后求出∠BEP=90°,判定③正确,根据等腰直角三角形的性质求出PE,再利用勾股定理列式求出BE的长,然后根据S△APD+S△APB=S△APE+S△BPE列式计算即可判断出④正确;过点B作BF⊥AE交AE的延长线于F,先求出∠BEF=45°,从而判断出△BEF是等腰直角三角形,再根据等腰直角三角形的性质求出BF的长为
,判断出②错误.
| 2 |
解答:解:在正方形ABCD中,AB=AD,
∵AP⊥AE,
∴∠BAE+∠BAP=90°,
又∵∠DAP+∠BAP=∠BAD=90°,
∴∠BAE=∠DAP,
在△APD和△AEB中,
,
∴△APD≌△AEB(SAS),故①正确;
∵AE=AP,AP⊥AE,
∴△AEP是等腰直角三角形,
∴∠AEP=∠APE=45°,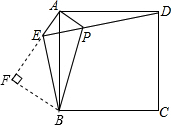
∴∠AEB=∠APD=180°-45°=135°,
∴∠BEP=135°-45°=90°,
∴EB⊥ED,故③正确;
∵AE=AP=1,
∴PE=
AE=
,
在Rt△PBE中,BE=
=
=2,
∴S△APD+S△APB=S△APE+S△BPE,
=
×1×1+
×
×2,
=0.5+
,故④正确;
过点B作BF⊥AE交AE的延长线于F,
∵∠BEF=180°-135°=45°,
∴△BEF是等腰直角三角形,
∴BF=
×2=
,
即点B到直线AE的距离为
,故②错误,
综上所述,正确的结论有①③④.
故选A.
∵AP⊥AE,
∴∠BAE+∠BAP=90°,
又∵∠DAP+∠BAP=∠BAD=90°,
∴∠BAE=∠DAP,
在△APD和△AEB中,
|
∴△APD≌△AEB(SAS),故①正确;
∵AE=AP,AP⊥AE,
∴△AEP是等腰直角三角形,
∴∠AEP=∠APE=45°,

∴∠AEB=∠APD=180°-45°=135°,
∴∠BEP=135°-45°=90°,
∴EB⊥ED,故③正确;
∵AE=AP=1,
∴PE=
| 2 |
| 2 |
在Rt△PBE中,BE=
| PB2-PE2 |
|
∴S△APD+S△APB=S△APE+S△BPE,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
=0.5+
| 2 |
过点B作BF⊥AE交AE的延长线于F,
∵∠BEF=180°-135°=45°,
∴△BEF是等腰直角三角形,
∴BF=
| ||
| 2 |
| 2 |
即点B到直线AE的距离为
| 2 |
综上所述,正确的结论有①③④.
故选A.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理的应用,综合性较强,难度较大,熟记性质并仔细分析图形,理清图中三角形与角的关系是解题的关键.

练习册系列答案
相关题目
 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 一点,连接AP.过点P作PF⊥AP,与∠DCE的平分线CF相交于点F.连接AF,与边CD相交于点G,连接PG.
一点,连接AP.过点P作PF⊥AP,与∠DCE的平分线CF相交于点F.连接AF,与边CD相交于点G,连接PG.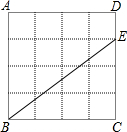 (2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.
(2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.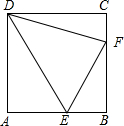 (2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.
(2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.