Question

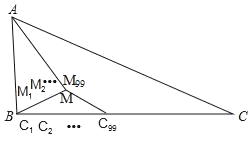
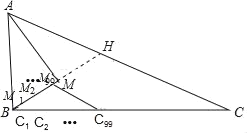
【题目】如图：△ABC中，AM平分∠BAC，且AM⊥BM于点M，已知AB＝8，AC＝20，M1、M2…Mn﹣1把线段BM分成n等份（其中n为正整数），C1、C2…C2n﹣1把线段BC分成2n等份，则M99C99＝_____．

Answer 1

【答案】

【解析】

延长BM交AC于H．首先证明BM=MH，AB＝AH＝8，计算出BM＝BH，HC=12，然后由M99C99∥AC利用平行线分线段成比例定理解决问题即可.

解：延长BM交AC于H．

∵AM⊥BM，

∴∠AMB＝∠AMH＝90°，

∴∠BAM+∠ABM＝90°，∠HAM+∠AHM＝90°，

∵∠BAM＝∠HAM，

∴∠ABM＝∠AHM，

∴AB＝AH＝8，

∴BM＝BH，HC＝AC﹣AH＝20﹣8＝12，

∵M1、M2…Mn﹣1把线段BM分成n等份（其中n为正整数），C1、C2…C2n﹣1把线段BC分成2n等份，

∴M99C99∥AC，

∴＝，

∴M99C99＝12×＝，

故答案为．