Question

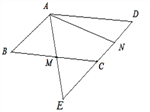
【题目】如图，在平行四边形ABCD中，M，N分别为BC，CD的中点，AM=1，AN=2，∠MAN=60°，AM ，DC的延长线相交于点E，则AB的长为_____________；

Answer 1

【答案】

【解析】分析：延长DC和AM交于E，过点E作EH⊥AN于点H，易证△ABM≌△ECM，再证得AB=NE，因为AN=2，AE=2AM=2，且∠MAN=60°，可得∠AEH=30°，AH=AE=1，根据勾股定理可得EH = ，EN=2，即可得AB=.

详解：

如图，延长DC和AM交于E，过点E作EH⊥AN于点H．

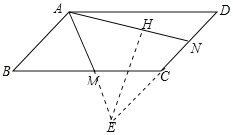
∵四边形ABCD为平行四边形，

∴AB∥CE，

∴∠BAM=∠CEM，∠B=∠ECM．

∵M为BC的中点，

∴BM=CM．

在△ABM和△ECM中，

，

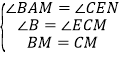∴△ABM≌△ECM（AAS），

∴AB=CD=CE，AM=EM=4，

∵N为边DC的中点，

∴NE=3NC=AB，即AB=NE，

∵AN=2，AE=2AM=2，且∠MAN=60°，

∴∠AEH=30°，

∴AH=AE=1，

∴EH= = ，

∴NH=AN-AH=2-1=1，

∴EN==2，

∴AB=×2=；

故答案为：．