题目内容
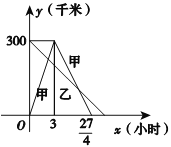
【题目】已知：甲乙两车分别从相距300千米的A，B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．
（1）求甲车离出发地的距离y甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
（2）若已知乙车行驶的速度是40千米/小时，它们在行驶过程中何时相遇？
【答案】（1）y=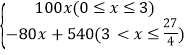
（2）两车第一次相遇时间为第
小时，第二次相遇时间为第6小时
【解析】分析：（1）由图知，该函数关系在不同的时间里表现成不同的关系，需分段表达．当行驶时间小于3时是正比例函数；当行使时间大于3小时小于
小时是一次函数．可根据待定系数法列方程，求函数关系式．
（2），由题意有两次相遇,分两种情况，列出方程解答．
详解：（1）当0≤x≤3时，是正比例函数，设为
x=3时，y=300，代入解得k=100，所以
当3＜x≤时，是一次函数，设为
代入两点（3，300）、（，0），得
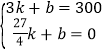解得 
，
所以
综合以上得甲车离出发地的距离y与行驶时间x之间的函数关系式为：y=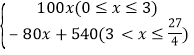
；
（2）由题意得甲车离出发地的距离y与行驶时间x之间的函数关系式为：
①当
，
，解得x=；
②当3＜x≤时，
，解得x=6．
综上所述，两车第一次相遇时间为第小时，第二次相遇时间为第6小时．
练习册系列答案
相关题目
