Question

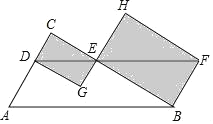
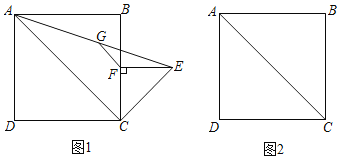
【题目】某课外活动小组准备围建一个矩形生物苗圃，其中一边靠墙，另三边用长为米的篱笆围成，已知墙长为米（如图所示），设这个苗圃垂直于墙的一边的长为米.

（1）垂直于墙的一边边的长为多少米时，这个苗圃的面积最大，并求出这个最大值；

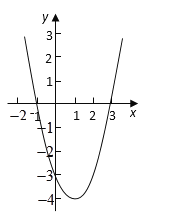
（2）当这个苗圃的面积不小于平方米时，试结合函数图象，直接写出的取值范围.

Answer 1

【答案】当垂直于墙的一边的长为6米时，这个苗圃的面积最大，最大值为72平方米；

【解析】

（1）设矩形苗圃的面积为S，根据矩形面积公式求出S与x的函数关系式，根据二次函数的性质，即可求得这个苗圃的面积最大值；

（2）求出苗圃的面积等于平方米时x的值，根据图象，即可求得苗圃的面积不小于平方米时x的取值范围．

解：（1）设矩形苗圃的面积为S，

由于这个苗圃垂直于墙的一边的长为米，则宽为（24－2x）米，

∴，

∴当x=6时，S取最大值72，且符合题意，

故当垂直于墙的一边的长为6米时，这个苗圃的面积最大，最大值为72平方米；

（2）当苗圃的面积等于平方米时，即，

解得：x1=4，x2=8，

由函数图像可得，当这个苗圃的面积不小于平方米时，x的取值范围为4≤x≤8．