题目内容
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.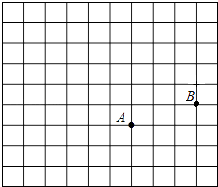
(1)建立适当的平面直角坐标系,使点A点B的坐标分别为(1,2)(4,3);
(2)点C的坐标为(3,6),在平面直角坐标系中找到点C的位置,连接AB、BC、CA,则∠ACB=°;
(3)将点A、B、C的横坐标都乘以﹣1,纵坐标不变,分别得到点A1、B1、C1 , 在图中找到点A1、B1、C1并顺次连接点A1、B1、C1 , 得到△A1B1C1 , 则这两个三角形关于对称.
【答案】
(1)
解:如图所示;

(2)45
(3)y轴
【解析】解:(2)如图所示,
∵AC2=42+22=20,BC2=12+32=10,AB2=12+32=10,
∴△ABC是等腰直角三角形,
∴∠ACB=45°.
所以答案是:45;
·(3)如图所示,由图可知△ABC与△A1B1C1关于y轴对称.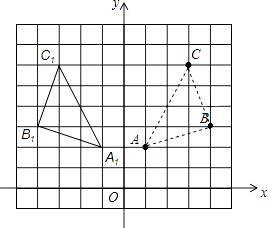
所以答案是:y轴

练习册系列答案
相关题目