题目内容
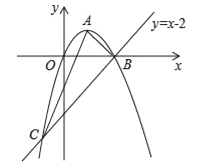
【题目】如图，直线l1的解析式为y=﹣2x+2，且l1与x轴交于点D，直线l2经过点A（4，0），B（0，﹣1），两直线交于点C．
（1）点D的坐标为；
（2）求直线l2的表达式；
（3）求△ADC的面积；
（4）若有过点C的直线CE把△ADC的面积分为2：1两部分，请直接写出直线CE的表达式．
【答案】
（1）（1，0）
（2）
解：设l2的表达式为：y=kx+b
根据题意，得 
解得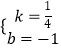 
所以l2的表达式为：y= 
x﹣1；
（3）
解：解方程组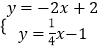 
，
得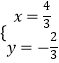 
，
所以点C的坐标为（ 
，﹣ 
），
过点C做CE⊥AD于点E，如图：
，
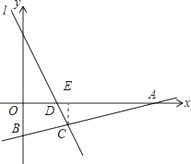
所以△ADC的面积为1；
（4）
解：当过点C的直线CE把△ADC的面积分为2：1两部分时，可得：DE：EA=2：1，或DE：EA=1：2，
可得点E的坐标为（3，0）或（2，0）
把（3，0）和（ ，﹣ ）代入解析式可得直线CE的表达式为 y= 
把（2，0）和（ ，﹣ ）代入解析式可得直线CE的表达式为y=x﹣2．
【解析】解：（1）把y=0代入y=﹣2x+2，可得：﹣2x+2=0，
解得：x=1，
所以点D的坐标为（1，0），
所以答案是：（1，0）；
【考点精析】掌握确定一次函数的表达式是解答本题的根本，需要知道确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
